Three dynamics: time-space, mass-charge, and electromagnetism-gravity

YellowArrow20x38YellowArrow-RightCENTER FOR PERFECTION STUDIES: CONTINUITY•SYMMETRY•HARMONY• USA•GOALS•August.2019
HOMEPAGES: ASSUMPTIONS|Bottom-up |DARK| INFINITY|Inflation |KEYS| MAP|Scholars|START

The Most-Basic Transformations

by Bruce Camber
Base-2 Model, Integrated Structure, Lemaître, Questions, Subject-Object, Time
Navigation: Links go to the Endnotes, Footnotes… 

Abstract: Three most basic functions, (1) cubic close packing, (2) period doubling, and (3) the Fourier transform, are each well-established within mathematics and the sciences. If taken together at the Planck scale, hypothesized to be a redefinition of the very nature of the Planck scale, there are inherent structures and dynamics that manifest, primary among them being an infinitesimal, primordial “shell” sphere. These structures-and-dynamics (forms-and-functions) are a very different map of our universe. An outline of that map is created by applying base-2 to the Planck base units. The resulting 202 doublings or base-2 notations† provide a very-simple,  mathematically-integrated look at our entire universe from the Planck scale, especially Planck Time to the Age-of-the-Universe-right-now. Captured by Euler, here is a model for emergence and natural inflation. Very few scholars are aware of these 202 doublings, and even fewer recognize that first 64 doublings of those Planck units are well below the space and time thresholds by which particles and waves are currently defined and measured. Proposed is a mathematical physics, perhaps called a foundational mathematics and physics, both progressively working within each of those first 64 doublings, building successively upon the other, and in so doing, redefining light, space, time, mass, energy, electromagnetism, gravity and infinity.

Brief Background History

Cubic close packing. Knowledge of cubic close packing goes back to Thomas Harriot (circa 1587), Johannes Kepler (circa 1611),  and Johann Carl Friedrich Gauss (circa 1801). More recently, through the work of Thomas Hales (1998, 2014), we learned that these scholars were each proven to have calculated a very good approximation of sphere-packed densities. Also, notably, in the 2010 Wikipedia’s summaries of this discipline inspired a programmer to create a simple, but highly-informative simulation of sphere stacking.1

Period doubling bifurcation. In 1885 bifurcation theory was introduced to the world by Henri Poincare; he set the foundations so nonlinear dynamics and period doubling bifurcation naturally evolved. In 1975 Mitchell Feigenbaum discovered two constants that opened the study of dynamical systems to wider audiences that now included Mandelbrot’s work on fractals, the Santa Fe Institute and their work on complexity and chaos theory, and Stephen Wolfram on computational irreducibility. In 2006 Ari Lehto refocused his work as he explored period doubling at the Planck scale and in 2014 Charles Tresser added insights regarding its universality. Yet, mechanisms to trigger period doubling have not been well understood. Our simple solution: consider sphere stacking to be the doubling mechanism for period doubling bifurcations,2 particularly at or near the Planck scale.

Fourier series and Fourier transform. Joseph Fourier did his primary work on the theory of heat in 1822 when he showed that some functions could be understood to be an infinite sum of harmonics. Since that time there have been thousands of scholarly papers about the Fourier series and Fourier transform. In 1963, Richard Feynman made it part of the focus of Chapter 50 of his infamous Feynman Lectures. Today, applied to a diverse array of applications from solving differential equations to signal processing to spectroscopy, the spectral analysis of a time series appears to be well understood. Yet, less understood is the infinitesimal scale, especially what happens when the Fourier transform is applied to, or close to, the Planck scale.3

Quick Summary: These dynamics are our platform to re-engage the Planck Scale.4

The Planck Scale

Max Planck introduced his fundamental units within his 1906 book, the Theory of Heat Radiation. 4a The most-simple ratio for Planck Time — 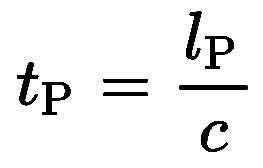screen-shot-2016-12-11-at-10-36-16-am — went unexplored. In 1964 C. Alden Mead finally had an article published that used the Planck Length. Titled Possible Connection Between Gravitation and Fundamental Length (Phys. Rev. 135, B849, August 1964),4b it had been held up in peer review for over five years. Nobody quite understood the Planck base units. Mead’s article is the first-known to be published to use the Planck Length. In 1982 John D. Barrow wrote an article, Natural Units Before Planck,4c mostly a quick study of George Stoney’s work as a precursor for Max Planck’s work to define basic units. In 1985 Thanu Padmanabhan, wrote Physical significance of Planck length 4d (Annals of Physics, Volume 165, Issue 1, November 1985, Pages 38-58). In 1992, John Archibald Wheeler compiled Physics at the Planck Length,4e International Journal of Modern Physics A, Vol. 08, No. 23, pp. 4013-4018 (1993). In 1998 Joseph Polchinski published Quantum Gravity at the Planck Length.4f And, in 2001, Frank Wilczek4g wrote a series of three articles for Physics Today (Scaling Mount Planck, I, II, and III ) about the Planck units and finally the rest of the scientific community really began to take note.4h In 2011 we began exploring the Planck base units and in 2012 noticed that that the Planck doubling for the speed of light was confirmed between the 143rd and 144th notations.4h

What if questions

What if time is understood to be finite, discrete, quantized, and derivative? What if there is an alternative to big bang cosmology with its infinitely hot start? And, what if there is an actual cutoff for quantum mechanics and fluctuations? What if there are no fluctuations below perhaps as low as the 20th, yet perhaps as high as 40th or 50th doubling? What if the word, quantum, as we currently understand it, just doesn’t apply to a range of the earliest notations?

What if our historical bias for waves and particles obscures our vision of other possibilities that may well only be embedded within math and logic?

What if within each notation, each doubling of the Planck Time and Planck Length, there are particular, even unique, dynamics? What if the first 64 notations are primarily geometries and dimensionless constants that give rise to homogeneity and isotropy? What if light is actually the concrescence of Planck Time, Planck Length, Planck Mass, and Planck Charge? What if every notation is active now and forever? What if all time is now?

Yes, what if we ask, “What happens?”

I conclude that we discover that the universe is a very relational place.5

Cubic close packing of equal spheres6

Sphere to tetrahedron-octahedron couplet

Spheres & Sphere Stacking. What is fundamental? John Wheeler reopened this historic question in a new way when he imagined quantum foam.6a Others say a sphere and some call them planckspheres.6b It seems to follow that the only thing light can become (as Planck Time, Planck Length, Planck Mass, and Planck Charge) is a sphere. Of course, this pre-particle substrate of a particular length–time-mass-charge needs a name. Being generated faster than any other process in the physical universe,  these spheres6c create endless strings;6d and, here would be the edge of the current expansion of the universe. Within Wikipedia6e the discussion about cubic close packing of equal spheres includes the illustration on the right. It was introduced in 2010 and demonstrates sphere stacking, a simple type of doubling that would appear to be the beginning of all period doublings.6f

This dynamic image also demonstrates the most simple relations between spheres and the beginnings of the simple geometries of tetrahedrons and octahedrons. As in music, we call it a tetrahedral-octahedral couplet.7 Octahedrons manifest in between any group of eight tetrahedrons connected at their vertices.  Within this dynamic image just above, the bottom half of the octahedron sits between any three tetrahedrons (red in the illustration above). Here are rather new foundations for old geometries. In this most simple iteration, plates of squares, and triangles (and hexagonals) are created that tile the universe. These 3D couplets also perfectly tessellate the universe.

When things start simply, the geometries are simple, but complexity quickly evolves within just a few steps or doublings.

From the first second to the first year.8 To create some perspective about complexity within this model, it is good to grasp the parameters of the four base units at one second and one year, between notations 143-and-144 and between 168-and-169 respectively.

At just over one second (1.2023 seconds at the 143rd notation), Planck Length is 360,424.632.km kilometers. To put that into perspective, the distance from the earth to the moon is between 406,700 km (252,700 miles) at the apogee and 356,500 km (221,500 miles) at the perigee. Starting with Planck Mass, the mass at 1.2 seconds is up in the range of a neutron star (see https://81018.com/a143/ ) which for many of us came as a fascinating surprise. At 4.1827×1025 coulombs, there is a substantial charge that originated from the doublings of the Planck Charge.

That is a lot of creation! In just over one second (and, if this model is anywhere close to the truth), something like it has gone on for every second of this universe!

Work to understand the first year between notations 168 and 169, or what might approximate a light year measured in seconds, has not yet been done. However, an introductory study of notation 167, approximately 116.73 days, has been started.

Well shy of a light year, the Planck Length doubling at the 167th doubling is now 3.0234609×1015 meters or 3,023,460,900,000 kilometers or 3.0234 trillion kilometers (1,878,691,504,115.963 miles). The diameter of our sun is 9.461×1012 kilometers or just 1.392 million kilometers. Experts argue that our Solar System is estimated to be as small as 4.503 billion kilometers across; others argue for over 23 billion kilometers. So, in just 116.73 days the universe is quite substantial — at least fourteen times larger than the  “large estimates” of our solar system using base-2 or simple doublings for 116.7 days.

The commonly-accepted measurement of a light year is 9,500,000,000,000 kilometers (9.5 trillion).  Within our chart it is 9,460,536,207,068.016 kilometers. We certainly are not quibbling. Proxima Centauri, the closest star to our own, is only 40 trillion kilometers (4.3 light-years) from our sun. And, it appears that the entire Milky Way galaxy is estimated to be 1 quadrillion kilometers across.

Now, just for reference, the four Planck unit doublings at the 169th notation are: 40,343,251.097 seconds, 1.209384×1013 kilometers, 1.628×1042 kilograms, and 1.403×1033 coulombs. The number of spheres has gone from the very first one to 1.8707×1050 spheres.

To say little more, in the course of just one second and 143 doublings or notations, the universe has become rather substantial. Yet, within just a year, much of our universe as understood today has begun to manifest. Yes, in just the first year of our universe, it is actually beginning to look a lot like our universe!

Even for us who have been studying these numbers since 2011, it is still hard to believe.

So, within this model, understanding the first second and the first year are pivotal. That simple little dynamic image above has been busy! Yet, within just 64 doublings, this sphere stacking defines a grid, matrix or aether that is well below any possibility to measure the actual Planck Length or Planck Time doubling. Notwithstanding, mathematically those first 64 notations appear to be rather comprehensive and pivotal.

Period doubling bifurcation theory 9

In the early years of this study of the 202 doublings, our chart was a foot wide and five feet tall. It was a bit awkward at one’s desk so a table top version was envisioned. Finally, in December 2013, a simple 11″ by 11″ chart was laid out.9a The first 60 notations are in groups of ten outlining the infinitesimal or small-scale universe. Also, there are 50 groups that outline the large-scale universe, notations 141 to 190.

The period doubling from Notation 1 to Notation 60 were of particular interest. Nothing was there!

To begin to get a grasp of its potential definition, the Greats were summoned. In the first grouping 2-10, Plato’s concept of forms was instantiated.9b For notations 11-to-20, a Bourbakian sense of structures was engaged.9c Aristotle’s concept of Ousia or Substances, a precursor of the Periodic Table was intuited for Notations 21-to-30.9d Qualia (or pure qualities) was also imagined between Notations 31-and-40.9e Relations (versus the derivative, subject and object) were intuited within Notations 41-to-50.9f At some one of these ten notations, and probably not one of the primes, a geometry of imperfections begins with the simple object created by five tetrahedrons with its gap of 0.12838822 radians (a 7.356103 degree gap).9g The next group of notations, 51-to-60, is designated, Systems, and opens up systems theory, including all the studies of consciousness.9h Within the notations 61-to-65 the face and functions of elementary particles should be shaping up for emergence.

Doublings. In this data stream, a third approach to these concepts is the study of period doubling, bifurcation theory, coming full-circle with our first, most-simple, doubling mechanism, cubic close packing of equal spheres. Here that mechanism is described as stacking. There are other types of doublings, but there appears to be no other doubling mechanism per se. In Finland, physicist Ari Lehto claims that the period doubling mechanism is a universal property of nonlinear dynamical systems and that it governs the buildup of structures; he says, “…from the intrinsic properties of the elementary particles to the large scale systems with cosmological dimensions.” In our model here, Lehto is asked to consider those notations or doublings prior to elementary particles.

Lehto writes, “The mechanism that indicates a high degree of order in nature is not a part of the prevailing theories but it could give a major contribution to our understanding of the physical reality and the origin of the invariant properties and structures of matter.” 9i

The Fourier transform10

True confessions.10 Because I do not have anything close to what would be considered a baseline for writing this analysis, the following postulations are simply my guesses more than based on a deep-and-rich understanding of these functions.

Symmetries in motion. The circle-sphere dynamics now transition from basic geometries, to symmetries in motion.

The work of a wide range of people, from Pythagoras (c. 570 – c. 495 BC) to Feynman (1918-1988) to Strogatz (1959-  ) to today’s thinkers and tinkerers within music theory, may find a key function and a new paradigm within the Fourier transform understood from the Planck scale.

File:Circle cos sin.gif

There is an inner transformation (pictured, above right) that I would equate to electromagnetism, Maxwell’s equations and Faraday’s intuitions. Then there are the outer transformations which I would equate with the de facto dialogue between Newton and Einstein and the current wrestlings regarding our understanding of gravity and loop quantum gravity (LQG).

See Sir Martin Rees’ Just Six Numbers.

The internal and external dynamic of spheres. The three dynamic images above are each, in their very special ways, based on our most ubiquitous, never-ending, never-repeating, dimensionless constant, pi.

If in the first emergence there are endless strings of spheres, could it also be a face of Planck Charge, Planck Mass, Planck Length and Planck Time? If part of that emergence is the inner transformation of pi, in what ways is it the face electromagnetism and an expression of Planck Time, Planck Length, Planck  Mass and Planck Charge? If another part of that emergence is the outer transformation, in what manner of speaking is this the face of gravity and yet another expression of Planck Time, Planck Length, Planck Mass and Planck Charge?

History will be a guide. How could so many applications not be tied to the fundamentals of our beginning?

A foundational mathematics and physics11

The foundations-of-foundations: A Quick Summary. If the first 64 notations are taken as a given, they certainly do not describe physical reality as we experience it or understand it today. Most people have a de facto absolute plenum of space and time within which everything exists and has its being.  Within this model of the universe, the infinitesimal spheres create space, time, mass and charge and these stack, causing a period doubling, thus causing dynamic symmetries to evolve with uniquely defined dynamics at each notation. Those notations or doublings defined by a prime number have an additional uniqueness to interject entirely new dimensionless constants into the overall doubling equations. It seems to follow that from one of these notations Langlands programs would begin to evolve, and then from another, string theory would evolve with its unique language and functions.  The nineteen prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67 whereby base-2 begins at 2, and our science of particles and waves begins at 67. What begins at 3? …at 5? …at 7? Which dimensionless constants can be applied; and then upon which of those can more mathematical structures be developed?

Perhaps a number theorist like Akshay Venkatesh of the Institute for Advanced Study can help us. Perhaps we need to go back and reintroduce ourselves to Robert Langlands, Ed Frenkel and other thought leaders among the Langlands group (Robert Kottwitz, Stephen Gelbart, Thomas Hales, Gerard Laumon, V.G. Drinfeld, D. Gaitsgory and others). Perhaps we need to reintroduce this conjecture to our string-theory thought-leaders like Edward Witten and Gabriele Veneziano and those testing their conjectures like Krzysztof Cichy….

Language. Because these first 64 notations appear in every way to be below the thresholds of measurement of space and time, there is a need to attempt to simplify set theory with  language, words and expressions, that capture the forms and functions that give rise to the realities we can measure. Wouldn’t it be fascinating to begin to be able to make distinctions between reification, instantiation, hypostatization, and hypothesization? It just may be possible.

Dimensionless constants. All the key dimensionless constants, particularly those considered to be necessary for the Standard Model for Particle Physics, will have a very special role, especially when each is considered a bridge between the finite and infinite. 11

Finite-Infinite12

Although lightly approached within several documents within this website, it is now increasingly obvious that the mathematics, science and philosophy of renormalization12 needs to be further explored. To deny infinity is to know infinity. So, infinity, both mathematical and conceptual, can be uniquely and independently known through the use of renormalization within any of the sciences, especially physics, and mathematics.

Since the renormalization work of Dyson, Feynman, Schwinger and Tomonaga (1947-50), Nikolay Bogolyubov, Stueckelberg and Petermann (1953) and the work of Wilson, Kadanoff, Fisher (1965 and 1975), scholars have developed ways to capture points within equations whereby infinity becomes equal to 1. Each is a possible clue. Beginning with with Freeman Dyson’s work in and around 1947, renormalization continues to be refined and expanded. In 1973  the Coleman–Weinberg potential was introduced.  Weinberg (1993), Dütsch (2013) and others continue that effort.

As with dimensionless constants, every new twist for renormalization demarcates a possible new entry point along the grid especially within the first 64 doublings, yet including the twenty-five primes between 67-and-199, i.e.  71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, and 197.

Renormalization was a welcomed relief from having to wrestle with infinity. Also, because the concept of infinity was so often associated with religious belief, it was a relief from those discussions as well. Some of our leading scholar-physicists went so far as to advocate that space, time and infinity be retired from academic inquiries. Within this model, these three pivotal concepts are further defined and refined. First, the simple doublings create continuity equations for each of the Planck base units creating a heretofore unrecognized definition of order, relations (symmetries) and dynamics (harmonics) that redefine the infinite and bind the finite and infinite.

These studies are just beginning. It is all still quite a general overview of possibilities.

Thank you.

###

Endnotes, footnotes, references and resources:

† Acknowledgement: In 2011, out of total naïveté, we used the Planck constant as given and not the reduced Planck constant. Over the years, we have had scholars question if it would have been better if we had used the reduced Planck constant. We are entirely opened to that discussion. If the consensus is that the reduced Planck constant would render better results, all the charts will be reworked and new charts posted. However, the basic concepts do not change. It would appear that about 22 additional notations would be added with the reduced Planck constant, yet everything will scale proportionately.
__________________

Sphere to tetrahedron-octahedron couplet

Sphere stacking

1 Sphere stacking: In 1587 the most efficient stacking of cannonballs was addressed by Thomas Harriot and then in 1611 by Johannes Kepler. It took over 200 years before Johann Carl Friedrich Gauss actually started to prove these conjectures and about another 200 years before the conjectures were more formally proven by Thomas Hales (website) and his people (2014). This question about density had become a key mathematical challenge, deemed by David Hilbert in 1900 to be the eighteenth problem; there appears to be no references to the size of the spheres. For example, I would ask, “Is it possible to have a sphere the size of the Planck Length?” Given the ineffable work of pi, I would argue, “Yes,” and begin sphere stacking at the Planck scale.

At this time the best possible visual of sphere stacking is further introduced.

Now about that name for this pre-particle substrate of a particular Planck length, Planck time, Planck mass and Planck charge…  what do you think of the word, letimach? No. It won’t do. I don’t like it either. Now you should know that I have total disdain for made up new words, so I am not anxious to introduce this silly word. I am sure the mathematicians among the Langlands programs and string theorists have enough vocabulary to share. I am confident that the right concept is already out there somewhere.
__________________

2 Period Doubling of Equal Spheres: Henri Poincaré was perhaps the first to provide a detailed description of period doubling bifurcation with his section, maps, and metrics. Mitchell Feigenbaum discovered precise values for when there is a bifurcation, a ratio of convergence (4.669201609…) which I believe is intimately related to sphere stacking. In 2008 Ari Lehto opened his exploration of period doubling at the Planck scale and in 2014 Charles Tresser opened explorations about its universality.

Explorations of period doubling within this article continue here.
__________________

3 Fourier transform: Perhaps the transform is one of the best known studies with the most diverse applications yet understood by the fewest people! There are two key dimensionless functions of the transform that I believe bear further scrutiny. Yet, to be sure, all of the work with the Fourier identity and transform is worth the time to get to know! Though I may have spent a little time in 1964 with Fourier’s work in introductory physics classes, it has only been reintroduced to me by Stephen Strogatz’s scholarship; however, there is so much more to learn about all the applications.

In his book, Just Six Numbers, Sir Martin Rees’ first number is “…the ratio of the fine structure constant (the dimensionless coupling constant for electromagnetism) to the gravitational coupling constant, the latter defined using two protons.” He continues, “…(it) governs the relative importance of gravity and electrostatic attraction/repulsion in explaining the properties of baryonic matter…”  Our focus will be to see if there is a relation between the inner transformation and the outer transformation as an expression of the Fourier transform.

It is just a hunch.

This focus on the sine and sine wave in and around the Planck scale will extend to  Richard Feynman‘s incisive work within his infamous lectures. It is particularly helpful because he awakens the Fourier transform within the power of music with all its harmonics (pleasing perfections).

Beyond this simple introduction to its history, this Fourier analysis continues here. 
__________________

4 Platform for the Planck Scale: Since 2011 we have explored the Planck scale. Since 2016 this exploration has been compiled within this 81018.com website. This is the first time to consider the possible concrescence and transformations that could be occurring with cubic close packing, sphere stacking,  the Fourier transform, and period doubling. These dynamics raise rather unusual questions about this scale that began with Max Planck’s Theory of Heat Radiation 4a which was followed by the work of these key scholars:
4b C. Alden Mead, Possible Connection Between Gravitation and Fundamental Length (Phys. Rev. 135, B849, August 1964)
4c John D. Barrow, Natural Units Before Planck, Quarterly Journal of the Royal Astronomical Society, Vol. 24, P. 24, 1983
4d Thanu Padmanabhan, Physical significance of planck length, Annals of Physics, Volume 165, Issue 1, November 1985, Pages 38-58  PDF (currently a distinguished professor at the Inter-University Centre for Astronomy and Astrophysics, (IUCAA), Pune, India)
4e John Archibald Wheeler, Physics at the Planck Length, International Journal of Modern Physics A, Vol. 08, No. 23, pp. 4013-4018 (1993).
4f Joseph Polchinski.  Quantum gravity at the planck scale (PDF), 1998 Polchinski (ArXiv)
4g Frank Wilczek Physics Today (Scaling Mount Planck, I: A View from the Bottom June 2001, II: Base Camp, November 2001, and III: Is that all there is? June 2002 Also, consider this key section of the Wilczek et al article on fundamental laws.
4h  81018.com All the formulas for the Planck scale became a primary study for us.

__________________
5 Postulations: Light is the concrescence of Planck Time, Planck Length, Planck Mass, and Planck Charge. There may be ways to test this speculative claim. With this construct out in the public’s view, perhaps someone will now volunteer a suggestion. This article is more of an appeal to consider a new model of the universe by opening just enough plausibility that it becomes part of the current discussions.  The words, a very relational place, reflect the ever-so-short Newton-Leibniz debate known through Samuel Clarke’s book,  The Leibniz-Clarke Correspondence whereby Newton’s absolute space and time are rebuked by Leibniz in favor of a dynamic relation. Though Leibniz point of view is often contrasted with the container theory, the 202 notations create a new radical relational container within which relativity has its place.
__________________
6  Cubic close packing of equal spheres: Can a sphere manifest at the Planck scale? Could it be the most basic thing that defines space and time? Age-old questions with many faces, yet to date, there has not been a redefinition of the sphere in a way that qualifies it as an actual thing below the thresholds of space and time measurements. In 1955 John Wheeler suggested quantum foam. That was a new concept.  The next step would be the concept of a plancksphere. It appears to have first emerged in 1999 in an article by D.V. Ahluwalia, On Quantum Nature of Black-Hole Spacetime: A Possible New Source of Intense Radiation, page 4. Though not widely used, it was again used in the 2013 proceedings (page 379) of the annual meeting of the Natural Philosophy Alliance. Then, the use of the term began popping up with some regularity. Once the sphere is engaged at the Planck scale (and in this model it has 64 doublings to go before it has any semblance of a particle, wave or fluctuation), a door is opened; we just might begin to grasp a deeper understanding of spheres as we continue to ask more questions, i.e. “What does a sphere have to do with string theory?” …with Langlands programs?

In January 2016 that simple dynamic image of sphere stacking was used. That image within Wikipedia brought simple geometries alive well before particles and waves and opened the relation between the simplest 3D object and points, lines and triangles.

David Bohm would have loved it!

_________________________________________________________________________
7 Tetrahedral-octahedral couplet: New foundations for old geometries. Yes, the first place this construction was used within this website was early in 2016 within this analysis of numbers. Even before these studies, our geometry students were heavily engaged with basic models using the platonic solids: https://81018.com/tot/ We had observed the triangular, square, and hexagonal tilings and tessellations:  https://81018.com/2014/12/01/tiling/  It had been frustrating to think that simple things were not part of our theories of who we are and why. Now these concepts were not only integrated, but became pivotal. 
______________________________________
8 The first second and the first year: These simple numbers have been difficult to internalize. Where the big bang theory has not been able to get much behind the first 300 million years (our notation 197), our chart is mostly about the earliest universe. Yet, our halfway point, Notation 101, is defined by 40.95 microns, 5.51×1021 kilograms, processing at 1.366×10-13 seconds, is still non-intuitive to me. If it is taken as a given that each notation is active now and forever, Notation 101 is the beginning of the human condition, yet how does that work with Notation 202 within which we are currently defined. That challenge continues. To begin to grasp these new textures, we’ll need to have a more comprehensive understanding of the first 64 notations.
___________________
9 Period doubling: Nine key concepts within this section will be further developed. We have barely smudged the surface. The anticipation, perhaps a hope or a dream or fantasy, is that all those disciplines (and all their scholarship) that have been off the grid and in their own silos will eventually discover a place within particular notations or range of notations.
9a The December 2013 chart will eventually be updated so every notation has its own box and that box will click through to an ongoing analysis
9b Plato’s concept of forms was instantiated between notations 2-10.
9c A Bourbakian sense of structure was engaged for notations 11-20. More...
9d Aristotle’s concept of Ousia or Substances, a precursor of the Periodic Table was intuited for Notations 21-30.
9e Perhaps the essence of qualities, Qualia (pure qualities) are between Notations 31-40.
9f The concept of Relations (versus the subject– object) were intuited for Notations 41-50.
9g This model anticipates that at some one of these notations (and probably not one of the primes), a geometry of imperfection most simply begins with the simple object created by five tetrahedrons with its gap of 0.12838822 radians (7.356103 degree gap). The question should be asked, “Are there precursors of quantum fluctuations?”
9h The next group of notations, 51-60, is designated, Systems, and opens up systems theory, including all the studies of consciousness and brain-mind relations.
9i Ari Lehto’s work gives me some hope that we are on a the right path.

___________________________
10 The Fourier transform: Cornell mathematician, Stephen Strogatz, loves the Fourier transform and I thank him for his spirited re-introduction to its place within science and with the functions of pi.  If by starting at the Planck scale, the Fourier transform redefines electromagnetism and gravity, our best living scholars throughout the breadth and depth of all those applications will be encouraged to engage this construct. More…

Key Fourier applications just may be extended in ways to address age-old questions. I have a hunch that there are calculations between the inner and outer transformations that just might confirm Sir Martin Rees first number within his book, Just Six Numbers. It is the ratio of the strength of the electrical force to the gravitational force. Surely this might add an important twist to our understanding of gravity and charge and mass.
___________________________________________
11 Foundational Mathematics & Physics: Here we will work on a highly speculative hunch, perhaps just a bit more silliness, whereby all the mathematics of Langlands programs, string theory, and even renormalization get pulled into the grid and a door is opened to the infinite and our multiverses whereby continuities (order), symmetries (relations) and harmonies (dynamics) become part of the definition of the bridge between the finite and infinite. Some of the scholars whose work is being studied are:

Of course, the role of the dimensionless constants — the first 26 identified by John Baez, the 31 identified by Wilczek, Tegmark, Rees, and Aguirre (TOE), the other 104 dimensionless constants defined within Wikipedia, the 300+ defined by the National Institute for Standards & Technology (NIST) (PDF – 2008, SI Report), and 11.3 billion, computer-generated, mathematical constants defined by Simon Plouffe — will all eventually be considered and slotted or applied to notations, 1-64 or forms 9b to 9h.

_________________
12 Finite-Infinite: What is held in common by every “successful” renormalization? Do we have a philosophy of renormalization12 that respects both the finite and the infinite? Does each  formula tell us something quite special about the infinite? Is it possible the infinite can be known through the equations within renormalization? We’ll explore answers to these questions through the work of the following scholars:

We take as a given that the infinite is a composite of these dynamic qualities:

The 202 notations has been characterized in the very early years of this work as a “BIG BOARD–little universe” simply because the first 144 notations are all within the first second of the universe. Can we use set theory, group theory and prime-number base notations to explore further how the next 57 notations could be navigated equally fast?  Also, let us all be looking to see how any entity within the current moment of the 202nd notation are a composite from within virtually every notation.  With such a conceptual framework for time,  of course, the concept of a wormhole and a blackhole will begin to morph.

###

______________________________________________________

Background. Closely-associated with other homepages, this article will continue to be updated. Four homepages are related: Transformation (August 2019), Bottom-up (September 2019), Twelve Formulas (Oct. 2019), and Map the Universe (Oct. 2019).

_____________________________________________

Guesses & Hunches

1. What if  light is the concrescence of Planck Time, Planck Length, Planck Mass, and Planck Charge?  If so, is the face of light “time-space-mass-and-charge”?  How can light have four faces? How does cubic close packing, sphere stacking, period doubling, Fourier transform encapsulate it?

2. Brain-Mind-Consciousness: What if the brain is a simple storage device that is limited to approximately 24 hours? Perhaps the processing halves after sixteen hours until sleep releases it to recompile that data within the infinite-but-shaping the finite. If recompiling is a finite-infinite relation, then the finite-infinite relation is a necessary dynamic to define who we are and why.  There’ll be more to come…

3. Just Six Numbers, Sir Martin Rees. The first number is “…the ratio of the fine structure constant (the dimensionless coupling constant for electromagnetism) to the gravitational coupling constant, the latter defined using two protons.”

The relative importance. Gravity and electrostatic attraction/repulsion in explaining the properties of baryonic matter…”

Is there a relation between the inner transformation and the outer transformation as an expression of the Fourier transform?   More…

###

Please send along your comments or questions.

Continued Research:

  • Tresser: “Before metric universality was discovered, combinatorial and topological forms of universality were described for real maps, for instance in a theorem by Sharkovskii (1964) that remained too long mostly unknown (see also Metropolis (1973); Milnor and Thurston (1988), and RG-related ad hoc theories were to understand some of that (Gumowski and Mira, 1975; Derrida et al., 1978).”

Others:

The first derivative of position with respect to time is velocity, the second is acceleration, and the third is jerk. The fourth is snap or jounce, while the fifth and sixth are sometimes called crackle and pop.

Snap, the fourth derivative of the position vector with respect to time, or the rate of change of the jerk with respect to time; in physics,  it is also known as jounce. Equivalently, it is the second derivative of acceleration or the third derivative of velocity.

Conceptual foundations to bring these concepts together:

Building off this article on Dark Matter / Dark Energy

An excellent resource to translate any of our pages by its URL:
http://itools.com/tool/google-translate-web-page-translator

If you liked this page and website, please do not hesitate to follow us on Twitter or Linkedin.

History of this page:
• Privately-posted for development on July 23, 2019 @ 7 AM
• Publicly-posted as a working draft on July 25, 2019 @ 9 PM
• Most-active writing and editing, July 26-31, 2019
• Endnotes, footnotes, references and resources, periodically, July 30 – August 29, 2019