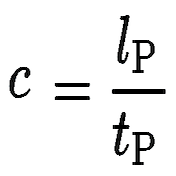CENTER FOR PERFECTION STUDIES: CONTINUITY•SYMMETRY•HARMONY•USA•Goals•2018
HOMEPAGES: ARISTOTLE|DARK|FORMULAS|HAWKING|KEYS|NEWTON |UP
72 of 202: A grid-matrix-system for everything, everywhere for all time, Not a theory or vision, just math
Editor’s Note: A five-part group of articles, the other four are as follows:
• Einstein would have gone even further if he had an integrated view of the universe.
• Our Open Letter To You: An introduction to a very simple chart of the universe…
• Concepts about which we can say, “These are our first principles.”
• Big Bang Theory Diffused
Emergence-Growth: Grasping the boundary conditions between the finite and infinite
By Bruce Camber, April 2018
Abstract: To understand the most simple form of emergence and growth still requires engaging a wide diversity of ideation including phase and scaling transitions, initial conditions, and boundary conditions, all between the finite and the infinite. Also, this analysis is set within work that started in December 2011 to define the 202 doublings (or 202 base-2 notations) from the Planck scale (Planck Length/Planck Time and Planck Mass/Planck Charge) through to the current size of the universe, age of the universe, mass of the universe, and charge of the universe. If the “infinitely dense, infinitely hot” conceptual framework can be diffused within a natural inflation, and the dynamics of emergence and growth become self-evident-and-simple, new questions and insights about the very nature of reality are opened.
Observation. At the time of this writing, only two references came up when googling the words, “boundary conditions between the finite and infinite.” Both refer to our earlier work. [1] Without those all-important “quotes” as delimiters, there are 242,000 references that discuss how combinations of those words apply to virtually every discipline under the sun. All have a common starting point. Yet, I have yet to become aware of an analysis by scholars of such a starting point between the finite and infinite. [2]
Visualizations of a common starting point. Two initial images open the analysis. Both have been analyzed within many pages of this website. [3] Though not widely affirmed, it will continue to be argued here, that these initial ratios-then-structures:
(1) create space-and-time,
(2) extend our understanding of the very nature of light,
(3) render the first space-time moment of continuity, symmetry and harmony (infinity), and
(4) create a foundation from which all things as things are made.
Our initial visualization is captured by the two images just above.
The 202 base-2 notations. In this study each of the 202 doublings (or notations) is taken separately to begin to discern the manifold and unique possibilities (diversity) of emergence and growth. [4] Within each doubling the logic from the prior doubling unfolds-and-enfolds in the next doubling. Here, my intuitions tell me for the first time that number theory becomes shape theory which becomes dynamic theory.
Pi. Given the special class that pi has among dimensionless constants, its simplicity and ubiquity call out for special recognition as the first manifestation within our continuity equations. [5]
Taken as a given. The Planck scale defines the first instance of a physical manifestation and the first illustration (above left) seems to be the best possible visualization of the first three steps; and the tetrahedral-octahedral image (above right) gives us clues for the next few steps.
Couplet. This tetrahedral-octahedral complex is currently called a couplet in the spirit of a literary expression, whereby two lines of verse, usually in the same meter and joined by rhyme, form a unit. It instantiates as a range of dynamics even within this most simple configuration and has a simple thrust.
Planckspheres. The concept of a Planck sphere (PlanckSphere or plancksphere) has been used by physicists and geometers who in some manner engaged the 1899 work of Max Planck to define fundamental natural units for length, mass, time and energy. [6] It all begins with the generation of one circle-sphere.
This it would seem is a key action of the first notation.
With each successive sphere, a progressive concept of space-time emerges. Within this model of the universe, spheres are being generated one at a time, just as imaged above, making the space-time, mass-energy that defines an expanding universe.
Can you picture this universe quite literally being constantly (the expansion of the universe) filled with indivisible spheres that have a very small energy and mass and are themselves so small and fast they seemingly penetrate everything instantly? In this model of the universe, here is the edge of creation, dark matter, dark energy, once known as the ubiquitous aether. Now, can we picture them organized by the most basic geometries? Could it be that these are the first three, always-active, always-present, notations that are constantly defining our universe? Could this be Neil Turok’s perpetual bang?
Formulas. The formulas that create this moment are many. The first, of course, is the ratio that defines the dimensionless constant known as pi. In this model that exquisite, never-ending, never-repeating ratio bridges the finite and infinite and it is first defined by Planck Length (the embedded link is an early attempt to understand it — we now read there are some who have defined Planck Length without the use of the gravitational constant) and Planck Time. Within this model complexification comes very quickly; and within this website, it will take awhile to unravel our earliest understanding of it. [7] Also, other dimensionless constants appear to be present. I believe in some manner of speaking, Euler’s identity is at work and that the universe is foundationally defined by exponentiation.
Speculations. The sole action of the first notation is to generate basic spheres; for now, these spheres are called planckspheres The piling on as imaged within that sequence defines the foundational notational activity of the #0 notation.
Being entirely speculative, the first doubling is the form of structure whereby the first lines and triangles and tetrahedrons are created and there is an emergence of projective geometries.
The second doubling (second notation) is the form for the tetrahedral-octahedral couplet and the earliest beginnings of Euclidian geometries.
Yes, it would seem that these are the footings for number theory, geometry, and rest of mathematics. Here are the foundations for the Langlands programs. Here are the makings for fractals. And, of course, I could go on and make even more outrageous statements, yet let us save that for another day.
These first three steps are quite enough to get a discussion going!
See A0, A1, A2, A3 for more. Why not? Why now?
Please note as of 7 May 2018: Many more scholarly papers are to be distilled regarding period-doubling bifurcation and boundary conditions. This page will continue to be updated as a result of incorporating the insights and knowledge of those scholars.
Endnotes & Footnotes:
[1] Both references are the same article; one is within this website and other in LinkedIn:
____ • Simple Logic & Math – Our Universe In 202 Doublings: https://81018.com/math/
____ • Simple | Bruce Camber | Pulse | LinkedIn
This discussion continues [a], [b], [c], [d], [e].
[2] This work unwittingly jumps out of the current flows of the scholarly community. It is idiosyncratic. Yet, being even more speculative, it seems to follow that these spheres are the foundations for the finite-infinite transformation, the homogeneous and isotropic nature of things, the historic struggles to define the aether, a grid, the matrix, or the plenum; and cosmic microwave background radiation, dark energy, and dark matter. There are triangular, square, and hexagonal plates the are created within that tetrahedral-octahedral complex that literally tile and tessellate the universe. You have to observe it to believe it.
[3] An image of the tetrahedral-octahedral cluster (on the top, on the right) was used in the original chart in December 2011. The students made many models like this one, however, the very first models like it emerged in 1997. The dynamic image on the left, using the Graphics Interchange Format (GIF), was first used in January 2016 within an article about numbers. There are many discussions about it.
[4] One of the goals of this project is to analyze each doubling (notation, step, group) and to link it to scholarly work that defines the notation better than any other. Even though the work started in December 2011, this project is still within its earliest stages of development.
[5] There are many analyses of pi within this website, however, our page for Pi Day on March 14 will be continually enhanced. It is not a static or historic page. Other pages include:
• Pi Day and Stephen Hawking
• Pi Day today
• More Pi Day
• Our original pi page
The four primary continuity equations begin with Planck Length / Planck Time and Planck Mass / Planck Charge and these will be tracked here: https://81018.com/introduction and https://81018.com/continuity here.
[6] Planckspheres. This link goes to a working reference page, nowhere close to a first draft, but a composite of source materials (hopefully with links to those materials), to be read, re-read, then ground up, churned, and ingested to see if some sense can be made of the work of many people who have struggled with these issues!
The first person to whom I turned is John Wheeler and his concept of quantum foam.
[7] Complexification. This work will open a new avenue to complexification as understood within mathematics as given by this link to Wikipedia’s work. The argument for simplicity and beauty is relatively short lived within this scale of the universe.
There are many articles within this website to help open these discussions.
Key pages to open questions/insights about the nature of reality:
http://81018.com
http:/81018.com/home
https://81018.com/chart
https://81018.com/goals/
https://81018.com/concepts/
https://81018.com/constant/
https://81018.com/redefinition/
https://81018.com/exponentiation/
https://81018.com/π/
https://81018.com/s4a/
https://81018.com/euler/
https://81018.com/prime/
https://81018.com/inertial-frame/
https://81018.com/finite-to-infinite/
https://81018.com/2017/10/16/eight/
Continued research for this article:
One usually knows when an article is complete. This article is not. It is hardly considered a first-draft. Here are just a few of the articles that are being reviewed:
• Uwe C. Täuber, Critical Dynamics (Cambridge University Press, 2014), Phase Transitions and Scaling in Systems Far From Equilibrium (Annu. Rev. Cond. Matter Phys. 2017. 8:1–27 doi: 10.1146/)
• Shape dynamics, A report about Julian Barbour by Dan Falk for PBS NOVA in January 2016
• Richard Fitzpatrick, Teaching notes from 2006-03-29
• Reviewing our history: Physics in the Twentieth Century, Victor Weisskopf, MIT Press, 1972, 1979
• The physics of reality: space, time, matter, cosmos Proceedings of the 8th symposium honoring mathematical physicist Jean-Pierre Vigier, August 2012 Editors, Richard L. Amoroso, Louis H. Kauffman, Peter Rowlands Editor’s note: In 1980 Camber studied with JP Vigier at the L’Institut Henri Poincaré (IHP) in Paris.
- Good science is not easy.
- Good science requires integrity and humility.
- False starts are probably a given.
- Nobody likes “your idea” more than you.
- For more… there is always more.
Richard Feynman constantly reminds us all: “The first principle is that you must not fool yourself — and you are the easiest person to fool.” from his Cargo Cult Science. Also published in Surely You’re Joking, Mr. Feynman! (p. 343)
Today’s key question: How do we market simplicity, real deep simplicity that raises complexity? Hawking and Newton started with the abstracted and complex and have confused us all for centuries.
###
Worldviews limit perspective 