Where Hawking’s Universe Meets Pure Mathematics
by Bruce E. Camber, First presentation of this article, 21 January 2026
The Discovery: Starting from a single Planck-scale sphere and doubling that number at each step, gauge symmetry groups emerge at specific notations where the doubling count, physical scale, and symmetry dimension converge. SU(2) at Notation 2. SU(3) at Notation 8. SU(5) at Notation 24 (matching the GUT scale). This is not numerology—it’s geometric necessity.
This page: https://81018.com/geometry-to-physics/
Jump to: Alternative • Hawking • Path • What This Means • Predictions • Explore • References
I. The Need for an Alternative
Why Current Models Fall Short
For nearly a century, we’ve been told the universe began with a singularity—an infinitely hot, infinitely dense point that exploded in a “Big Bang.” This story, refined through generations of brilliant physicists, has become scientific orthodoxy. Yet recent observations challenge its foundations:
- JWST reveals mature galaxies too early – Galaxies appear fully formed just 300 million years after the supposed Big Bang, when the standard model predicts chaos and disorder.
- The horizon problem persists – Regions of space that could never have communicated show identical properties, requiring increasingly elaborate inflationary mechanisms.
- Dark energy and dark matter – 95% of the universe consists of entities we’ve never detected, invented to make observations match theory.
- Fine-tuning everywhere – Dozens of constants must be precisely calibrated to impossible accuracy, suggesting either multiverse speculation or missing foundations.
These aren’t minor anomalies. They’re symptoms of a deeper problem: our cosmological model may be built on the wrong foundation.
A Geometric Alternative
What if the universe didn’t begin with a singularity, but with geometry itself? What if the fundamental forces aren’t arbitrary choices, but geometric necessities that emerge from the simplest possible starting point?
This website presents an alternative framework:
- Starting with one Planck-scale sphere
- Doubling at each discrete step: 2, 4, 8, 16…
- Following 202 doublings from Planck scale to the observable universe
- Generating gauge symmetries, particle physics, and cosmic structure as geometric consequences
No singularity. No inflation. No arbitrary constants. Just pure mathematics becoming physics.
“What if gauge symmetries aren’t arbitrary choices—but geometric necessities emerging from the simplest possible structure?”
II. Where Hawking’s Path Opens: A Hero’s Limitations
In 2016, Stephen Hawking posed what he called “the ultimate question”: “Where did the universe come from?” His answer: the Big Bang—”everything in existence, expanding exponentially from an infinitely small, infinitely hot, infinitely dense point.”
Hawking was arguably the most brilliant cosmologist of his generation. By the late 1970s, he had received the Albert Einstein Award and honorary degrees from Princeton, Chicago, and NYU. His work on black holes, Hawking radiation, and singularity theorems transformed our understanding of spacetime.
Yet even the greatest minds work within intellectual boundaries. Author John Boslough intimated this in his 1985 book on Hawking: brilliance does not imply completeness.
Hawking’s focus—general relativity, black holes, quantum gravity, singularities—was deep and revolutionary. But there’s little evidence he formally engaged with several domains of pure mathematics and geometry that operate independently of relativistic field theory and may actually precede and constrain physical cosmological models.
Eight Mathematical Foundations Missing from the Big Bang Framework
When we examine the first 1/100th of a second through a base-2 exponential lens—202 finite notations from Planck scale to present—eight critical mathematical domains become relevant. These weren’t part of Hawking’s published work, not through oversight but because the Big Bang paradigm’s singularity assumption makes them seem unnecessary:
- Langlands Programs & Automorphic Forms
Deep correspondences between number theory, geometry, and symmetry initiated at the Institute for Advanced Study (1967-68). These may structure early unification processes within Notations 10-20. - Geometric Gaps of ~7.356° (Aristotle’s Gap)
The irreducible tension between five-fold symmetry (icosahedron, golden ratio φ) and six-fold symmetry (hexagonal, cubic lattices). Measured precisely by Frank & Kasper (1958), extended by Jonathan Doye. This gap drives symmetry breaking, curvature, and differentiation—but is invisible within singularity-based models. - π and the Irrational Numbers (π, e, √2, φ)
Fundamental constants, especially the three facets of pi (π) — continuity, symmetry and harmony, generate intrinsic tension, proportion, and transformation within finite structures. Essential to emergent geometry, treated only illustratively in standard cosmology. - E₈ and Sophus Lie
Exceptional symmetry groups and Lie structures central to advanced gauge theories and unification—absent from Hawking’s theoretical development. - Functional Analysis
Mathematical tools bridging discrete and continuous systems, finite and infinite dimensions, and emergent continuity—rarely addressed in cosmological origin models. - Perfection and the Infinite
The transition between finite geometric order and infinite potential, reframing how “perfection” manifests in physical reality beyond singularities. - Natural Unit Systems
Planck base units, Stoney units, ISO equivalents—treated not as mere constants but as generative structures calibrated for Planck-scale processes. - Base-2 Sphere Doubling at Planck Scale
One Planck-sphere per Planck-time, stabilized by the four primary irrationals, demonstrated in the Planck Polyhedral Core—yielding discrete continuity without divergence.
These eight domains illuminate precisely the notations where Big Bang theorists themselves acknowledge limited insight: the mysterious first moments where quantum gravity, unification, and the origin of structure should emerge.
Hawking Opens the Door
This is not critique of Hawking—it’s recognition that his genius operated within a paradigm that assumed singularities as starting points. Once you accept an infinitely dense beginning, you naturally focus on what happens after that moment: expansion, cooling, particle formation.
But what if there was no singular moment? What if the universe has always been finite, geometric, and ordered—just unimaginably small at its beginning?
Hawking’s work becomes the bridge to something deeper: his questions remain valid, but the mathematical foundation shifts from singularity to pure geometric necessity.
III. The Geometric Path Forward
A. Starting Point: One Sphere
Notation 0: Begin with the simplest possible entity—one Planck-scale sphere (1.616 × 10⁻³⁵ meters). Not a singularity. Not a point. A sphere—the most perfect, symmetric three-dimensional form.
Notation 1: Double it. Now there are two spheres. A continuity condition is created.
Notation 2: Four spheres. They naturally form a tetrahedron—the simplest three-dimensional solid, the geometric foundation of all structure.
B. From Tetrahedron to SU(2): First Symmetry Emerges
At Notation 2, something profound happens:
- Four spheres → tetrahedron → four vertices
- Tetrahedron structure maps isomorphically to quaternion algebra: {1, i, j, k}
- Quaternion algebra = SU(2) group structure
- SU(2) = mathematical foundation of quantum spin and weak isospin
This is not coincidence—it’s geometric necessity. The weak force’s symmetry emerges directly from the structure of four spheres in closest packing.
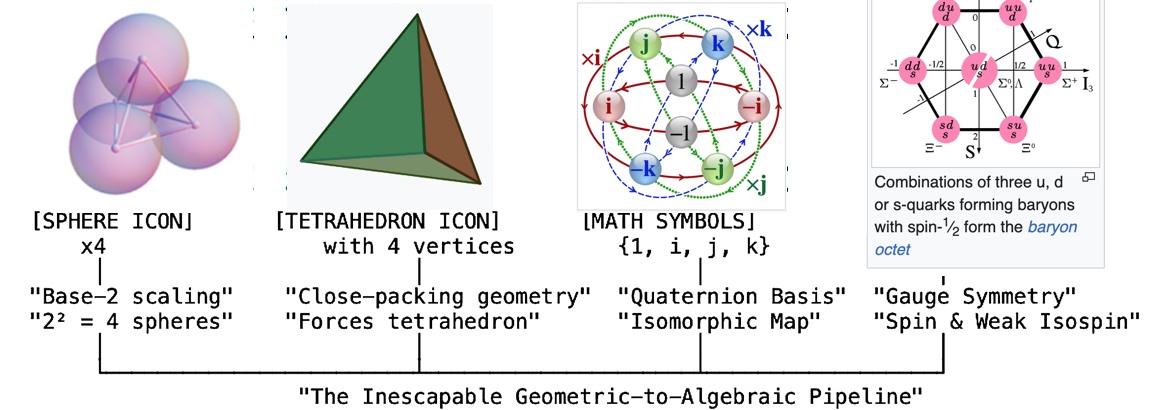
The inescapable pipeline from geometry to gauge symmetry: four spheres → tetrahedron → quaternions → SU(2). The weak force’s structure is encoded in the geometry itself.
See detailed derivation: “The Geometric Emergence of Gauge Symmetries”
C. The Pattern Continues: SU(3) and SU(5)
Notation 8: SU(3) Seed
- 2⁸ = 256 spheres
- Eight-fold symmetry patterns emerge naturally
- SU(3) has 8 generators → 8 gluons → color charge
- Foundation of the strong nuclear force
Notation 24: SU(5) Grand Unification
- 2²⁴ = 16.7 million spheres
- Physical scale: ~10⁻²⁸ meters (observed GUT scale)
- SU(5) has exactly 24 generators
- Three independent quantities converge: 24 doublings, GUT scale, 24 dimensions of symmetry
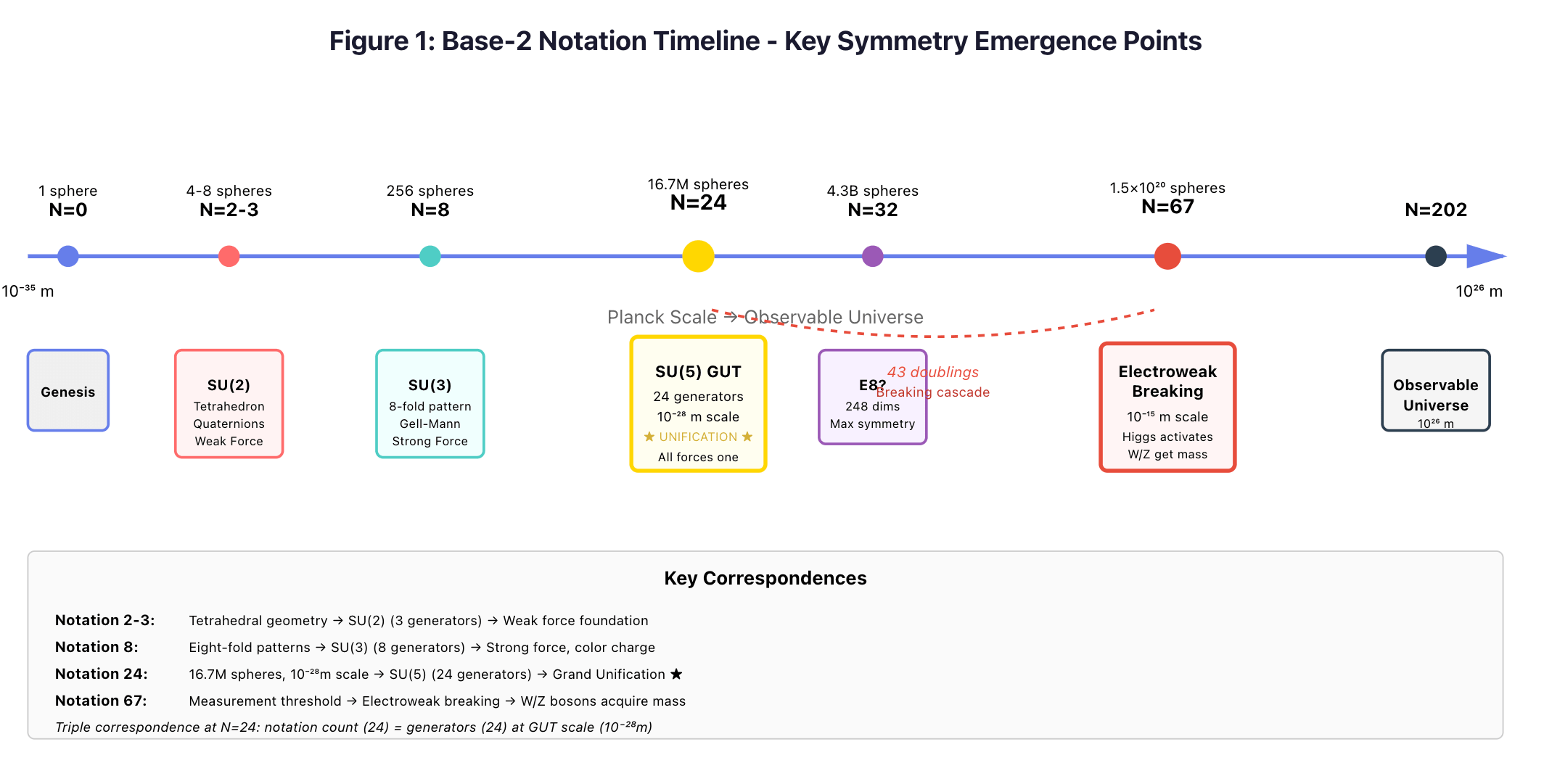
The complete journey: 202 base-2 doublings from one Planck-sphere to the observable universe, marking where symmetries emerge (SU(2) at Notation 2, SU(3) at 8, SU(5) at 24) and break (Notations 27, 67).
“At Notation 24, three independent quantities converge: 24 doublings from Planck scale, the observed GUT scale (~10⁻²⁸ meters), and SU(5)’s 24 generators. This is not coincidence—it’s geometric necessity.”
This is the heart of the discovery: the Standard Model’s gauge groups aren’t choices—they’re geometric inevitabilities.
D. The 7.356° Gap: Engine of Differentiation
Perfect symmetry would mean a static, crystalline universe—no change, no forces, no structure. But at Notation 2, an irreducible geometric tension appears:
- Five-fold symmetry (icosahedron, φ) cannot tile 3D space
- Six-fold symmetry (hexagonal, cubic) tiles perfectly
- The angular gap between them: 7.356°
Over 2400 years ago, it seems that Aristotle was the first scholar to postulate a universal role for the tetrahedron. He thought this most fundamental shape could be used to perfectly tile and tessellate the universe. If he had five tetrahedrons with equal edges and with all sharing one common edge, he would have observed a 7.356° gap. In 2022 we discovered the same gap is true for the octahedron. It wasn’t until 1958 that chemistry professors, Frank & Kasper, quantified it for the tetrahedron. That work continues today at Oxford and Cambridge through the work of Jonathan Doye’s group and their analyses within computational geometry.
This gap is not a flaw—it’s the creative tension that drives:
- Symmetry breaking (SU(5) → SU(3)×SU(2)×U(1))
- Curvature and non-Euclidean geometry
- The emergence of distinct forces
- The cascade from unity to complexity
Full analysis: “The 7.356° Gap: Natural Path from Geometry to Physics”
E. The Breaking Cascade: Notations 24-67
Once symmetries emerge, they must break to create the physics we observe:
Notation 24-26: SU(5) unified—all forces one
Notation 27: SU(5) → SU(3) × SU(2) × U(1)
– Strong force separates
– X and Y bosons become super-massive
Notations 28-67: 43 doublings of geometric tension
Notation 67: Electroweak breaking
– W and Z bosons acquire mass
– Higgs mechanism activates
– Scale: ~10⁻¹⁵ meters (matches observation)
The ratio from GUT to electroweak: 2⁴³ ≈ 10¹³
Observed in nature: 10¹¹ to 10¹⁴ (depending on measurement)
Detailed cascade: “The Breaking Cascade: Notations 24-67”
F. Beyond: 202 Notations to the Observable Universe
- Notations 0-10: Pure geometry, FCC packing
- Notations 11-24: Symmetries form
- Notations 24-67: Symmetries break, Standard Model emerges
- Notations 67-143: Particle physics, atomic scales
- Notation 143: A second exponential boundary—2¹⁴³ ≈ 10⁴³ (possible fractal structure)
- Notations 143-202: Molecular, biological, cosmological scales
- Notation 202: Observable universe horizon (today)
View the complete 202-notation map
IV. What This Means
1. A Universe Without Singularities
There was no “moment of creation” in the explosive sense. The universe has always been finite, geometric, and ordered—just unimaginably small in the very first instance of spacetime at Notation 0; it was one Planck-sphere. Then it doubled. And doubled again. And again.
This eliminates:
- The need for cosmic inflation
- The horizon problem (causally connected from the start)
- Initial condition fine-tuning (geometry is self-organizing)
- Arbitrary constants (they emerge from structure)
2. Forces Are Geometric, Not Arbitrary
The Standard Model asks: “Why SU(3)×SU(2)×U(1)? Why these groups?”
Answer: Because geometry at specific notations demands them.
SU(2) emerges at Notation 2 (tetrahedron → quaternions)
SU(3) emerges at Notation 8 (eight-fold patterns)
SU(5) emerges at Notation 24 (GUT scale, 24 generators)
The gauge groups aren’t selected from infinite possibilities—they’re geometric necessities.
3. The Langlands Program Has Physical Realization
The geometric Langlands program connects number theory, geometry, and representation theory. This model suggests these connections aren’t purely mathematical—they describe how geometry becomes physics from Planck scale to Standard Model.
Notations 1-24 may be where Langlands correspondences operate as the mechanism of symmetry emergence.
Explore: “Langlands Correspondences as Physical Mechanism”
4. Reality Is Comprehensible from First Principles
John Wheeler’s intuition was right:
“Behind it all is surely an idea so simple, so beautiful, that when we grasp it—in a decade, a century, or a millennium—we will all say to each other: how could it have been otherwise?”
This framework realizes Wheeler’s vision: beginning with one Planck-sphere and doubling 202 times, we generate the Standard Model’s gauge structure, particle spectrum, and cosmic evolution—without singularities, inflation, or arbitrary constants.
V. Testable Predictions
This is not speculative philosophy. The model makes specific, falsifiable predictions:
Energy Scales
- GUT scale: ~10⁻²⁸ meters ✓ (matches observation)
- Electroweak scale: ~10⁻¹⁵ meters ✓ (matches W/Z bosons)
- Scale ratio: ~10¹³ ✓ (within one order of magnitude of observation)
Symmetry Groups
- SU(2) from tetrahedral geometry ✓
- SU(3) from eight-fold patterns ✓
- SU(5) at notation matching dimension ✓
Mass Ratios
- Proton/electron ratio (1836) ≈ 2¹¹ (2048)
- Suggests 11-notation difference in emergence
Future Experimental Tests
- Look for signatures at intermediate notations (30-40)
- Test whether coupling constants relate to geometric ratios
- Search for 7.356° gap signatures in fundamental measurements
- Examine whether Notation 143 (second exponential boundary) has observable consequences
📊 For Physicists & Researchers
Key features of this framework:
- Predictions within one order of magnitude of observations
- Specific, falsifiable tests at multiple energy scales
- Geometric derivation of gauge symmetries previously treated as axioms
Technical resources:
VI. Explore Further
Core Model Pages
- The Geometric Emergence of Gauge Symmetries
- Notations 0-10: The Geometric Foundation
- Notations 0-24: From Planck Scale to Grand Unification
- The Breaking Cascade: Notations 24-67
- The 7.356° Gap: Natural Path From Geometry to Physics
- Langlands Correspondences as Physical Mechanism
- E8 and Maximum Symmetry at Notation-32
Mathematical Foundations
- The Irrational Constants: π, e, √2, φ
- Functional Analysis and Mathematical Physics
- Natural Unit Systems: Planck Base Units
- The Planck Polyhedral Core
The Complete Journey
- The 202-Notation Chart
- Base-2 Map from Planck Scale to Observable Universe
- Universe Map: Groups of 10 Notations
Historical Context
- The Manifesto: Continuity, Symmetry, Harmony
- Correspondence with Robert Langlands
- Correspondence with Edward Frenkel
VII. Join the Journey
This work challenges fundamental assumptions:
- That the universe began with a singularity
- That gauge groups are arbitrary choices
- That mathematics and physics are separate domains
- That complexity requires initial complexity
It suggests instead:
- Reality is profoundly integrative
- Geometry precedes and determines physics
- The universe is comprehensible from first principles
- The simplest starting point generates everything we observe
Ready to Explore?
- Start here: The Geometric Emergence of Gauge Symmetries — the mathematical derivation
- See the map: Complete 202-Notation Chart — Planck scale to present
- Deep dive: The 7.356° Gap — why imperfection creates complexity
VIII. References
- Four Irrational Numbers and Octahedral Plates: https://81018.com/hyper-rational-universe/ (retrieved 27 May 2025). Links π, e, √2, φ to octahedral plates. Supplemented by Coxeter, H. S. M. (1973). Regular Polytopes, Chapter 7, on octahedral geometry.
- Planck Units: NIST Planck Constant (https://www.nist.gov/pml/planck-constant, retrieved 26 May 2025). Supplemented by Misner, C. W., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation, Chapter 43, on Planck units.
- Qualitative Expansion Model: https://81018.com/qualitative-expansion/ (retrieved 27 May 2025). Defines QEM and four numbers. Supplemented by Weyl, H. (1952). Symmetry, on qualitative geometry.
- Continuity-Symmetry-Harmony: https://81018.com/integrity/ (retrieved 28 May 2025). On model’s principles. Supplemented by Weinberg, S. (1992). Dreams of a Final Theory, Chapter 5, on symmetry.
- Base-2 Notation: https://81018.com/chart/ (retrieved 28 May 2025). On 202 notations. Supplemented by Barrow, J. D., & Tipler, F. J. (1986). The Anthropic Cosmological Principle, Chapter 3, on exponential scales.
- Sphere Density: https://81018.com/tredecillion/ (retrieved 28 May 2025). On 18.5 tredecillion spheres. Supplemented by Conway, J. H., & Sloane, N. J. A. (1998). Sphere Packings, Lattices and Groups, on sphere packing.
- Dark Matter and CMBR: Steinhardt, P. J., & Turok, N. (2007). Endless Universe, Chapter 6, on alternative cosmologies challenging big bang models.
- Quantum Gravity: Rovelli, C. (2004). Quantum Gravity, Chapter 2, on Planck-scale spacetime, supporting lattice models.
- Ethics: Jonas, H. (1984). The Imperative of Responsibility, Chapter 1, on ethics in technological and cosmic contexts.
Contact: Research inquiries welcome → contact page
Principal Researcher: Bruce E. Camber
Website: https://81018.com
The first draft: Pure Perfection
Key model page: Gauge Symmetries
2025-26 homepage: Anniversary Homepage
