PERFECTION STUDIES: CONTINUITY•SYMMETRY•HARMONY • GOALS.•.October.2019
PERFECTION STUDIES: CONTINUITY•SYMMETRY•HARMONY • GOALS.•.October.2019
HOMEPAGES:.ASSUMPTIONS | BOTTOM UP | DARK| INFINITY | MAP-THE-UNIVERSE
THIS PAGE:.ASSUMPTIONS.|.FOOTNOTES |.REFERENCES |. EMAILS.| IM .| Zzzz’s
A Simple Mathematical Model of the Universe
by Bruce E. Camber A working draft: Everything, everywhere, for all time touched by infinitesimal spheres
Abstract: Stephen Hawking’s flavor of big bang cosmology blocked the view of a simple mathematical construct that encapsulates the entire universe within ordered relations. That construct provides an outline, possibly new foundations to see how part of the universe might have started very cold. It is surely a different approach to space-and-time, mass-and-charge, electromagnetism-and-gravity, and the finite-infinite relation. Perhaps simultaneously, another start which is infinitely-hot (Planck Temperature) is an instantaneous burst of light that then follows the inverse square law and begins to cool. It seems all these concepts are needed for the sciences, mathematics, and logic to unfold. This discussion focuses on twelve basic concepts to transition from Newton’s absolute space-time, the old big bang cosmology compression of all things, and the place of particles-and-waves to an infinitesimal, sphere-based model that gives rise to a finite, discrete space-time, quantum fluctuations and indeterminacy, and our universe as we know it. |
Background. Closely-associated with other homepages, this article will continue to be updated. Twelve Formulas (this page) is associated with Transformation (Aug. 2019), Bottom-up (Sept. 2019), Map the Universe (Oct. 2019), Finite-Infinite Bridge (Nov. 2019), Questions (April 2021) Starts (May 2021), Envision (May 2021), Empower (June 2021), Almost (December 2021), STEM (2013), the First Particle is Not a Particle (2022), A Simple Model (Aug. 2022), Most Simple (2023), and always the current homepage.
This article reviews twelve concepts* that seem foundational for this model:
1. Establish some boundaries.
2. Capture everything, everywhere, for all time.
3. Eliminate some basic mysteries: Dark energy and dark matter.
4. Start with the most simple and build. Complexity comes quickly. Redefine the infinite and the infinitesimal: Start with the equation for pi (π).
5. Follow the math and the simplest logic. Mathematically confirm the speed of light: Follow the numbers.
6. Force fit what you can. Compare their intellectual expansion to our mathematical expansion: The numbers are the numbers; logic is logic.
7. Analyze the logic. Examine six samples from across the 202 notations or doublings. Stretch.
8. The first sphere. Sphere stacking is at the heart of all doublings: Study this most pivotal image.
9. Open up period doubling bifurcation. Yes, we will all begin to get to know a rather imposing equation that begets this number: δ = 4.669 201 609 102 990 671 853 203 821 578
10. Test the Fourier series. Begin the Fourier transform dynamics at a primordial scale (i.e. the Planck scale).
11. This is where it is all going: We’re living in an exponential universe and among all things infinite. Let us continue studying Euler’s equations.
12. Geometries of probabilities and fluctuations. Study the geometries of gaps: Indeterminacy is geometrical.
__________
#1 Grasp the boundaries.
The Approximate Age of the Universe in seconds:
436,117,077,000,000,000± seconds1
436 quadrillion, 117 trillion, 77 billion seconds. A review of this very big number resulting from a rather simple mathematical exercise begins to give us a sense that the universe is finite. It has a starting point, the symbolic Planck base units; and it has an endpoint, the current time, the Now, always defined by the current expansion.
Within this model there is no absolute space and time. We surely envision a space-and-time that may well go on forever yet it has a starting point that is defined by its many relations which are primordial dimensionless constants represented by an equation.
What happens when we all know and can say, “The universe is somewhere just over 436 quadrillion seconds old!?!” If we all used a working Universe Clock (a little like the US Debt Clock), it just might help us all feel some commonality with each other within this world, with our little Solar System, then within the Milky Way and perhaps even our Local Group.*
What might happen when we all can begin thinking about everything we do and think in context with the entire universe? 1a
A Dilemma: In 2011 when we first engaged the question, the universe was estimated to be 13.772 billion years with an uncertainty of just 59 million years. That estimate continues to be more refined. Many now put the number closer to 13.81 while some as high as 14.4 billion years.
Yet, throughout the universe, how long is a year? We are on a Solar-Time System based on our Sun. The rest of the universe is not. Our year has 365 days except for Leap Year when it has 366 days. A simple question is, “For every thousand years, should we add 250 days?” We can all readily do the easy calculations — the number of seconds in a minute (60), an hour (3600), a day (86,400), and then a 365-day year (31,536,000 seconds). There are 31,556,952 seconds in a 365.2425-day year. And, 31,557,600 are in a 365.25-day year.
We chose 365.2425 days/year, 31,556,952 seconds/year or 31,556,952,000,000,000 per billion years (an aeon). Multiplied by 13.82 is 436,117,077,000,000,000 seconds.
At some point in the near future, we’ll be increasing that number. First, we’ll probably be multiplying by 14.1. Then we will need to add the approximate amount of time that will have passed from the moment the experts make their calculation. In 2011 we used the numbers from NASA’s Wilkinson Microwave Anisotropy Probe (WMAP).1b There is also ongoing work with the Hubble Space Telescope,1c the ESA Planck satellite,1d and NASA’s Spitzer Space Telescope.1e
Just a second: The value of a second was established by a consortium of government agencies around the world. In 1841 they unofficially began cooperating and sharing insights. In 1947 they formed the International Organization for Standardization1f (ISO) to share “official standards” but those standards were more fluid than most expected.
How does one define one second? The ancient approximation was 1/86,400 of the time that it takes the Earth to rotate once on its axis. In the 1700s it was determined by the pendulum swing of a carefully-calibrated grandfather clock, and then more recently by the very stable calibrations within the cesium-133 atom.
We’ve been advocating that the second be defined by an exact multiple of Planck Time. At Notation 143, it is .60116 seconds. Why not add that fraction that brings it as close as one needs to the current one second mark? We proposed such a concept back in 2012 when we advocated that a standard length be based between the multiples of the Planck Length. In 2012 we had the help of a NASA scientist, Joe Kolecki,1g He thought it was a worthwhile proposal for further consideration by the ISO.
Reviews: (1) Our 2017 analysis for Huntsville’s NASA SpaceApp: https://81018.com/universeclock/, (2) earlier calculations of an actual Planck time line, the 2016 horizontally-scrolled chart, and (3).the first calculations for time in 2014, a vertically-scrolled chart!
__________
#2 Capture everything, everywhere, for all time.
Apply base-2 to the Planck units:
202 notations from the first moment of time to the Now.2
2202 By definition, the Planck base units are key initial quantities of physical reality. Pi (π) and other dimensionless constants are part of the dynamics. Taken as a given, if these base units are doubled, then doubled again and again, in just 202 doublings, the current time (the Age of the Universe right now) and the current size of the universe (right now) are encapsulated. There are well over 1000 numbers that are generated within this chart (horizontally-scrolled). It is entirely predictive; each notation necessarily builds on the prior notation; and, all notations are never ending and never repeating. Symbolically, the very first instant of the universe is Planck Time: 5.391 16(13)×10-44 seconds. It is so infinitesimally small, the first second of this universe only emerges between notations 143 and 144. The first year emerges within notation 169. The first thousand years, a millennium, emerge between notations 178 and 179. The first million years are between notations 188 and 189; and, the first billion, an aeon, is between notations 198 and 199. Notation 200 has 2.744 billion years. Notation 201 has 5.4908 billion years. All of human history and most of the history of our Planet Earth are within Notation 202 (10.9816 billion years in duration). Given these notations appear to be cumulative, we would be in the earliest part of Notation 202 (13.81 billion less 10.9816 billion years).
For earlier perspectives, go to: https://81018.com/realization1/ https://81018.com/time/ https://81018.com/nature/ https://81018.com/newton/
_________
#3 Eliminate some basic mysteries.
Dark energy and dark matter:
Study those notations that cannot be physically measured.
264 The first 64 notations.3 We take as a given that all 202 base-2 notations defined within the horizontally-scrolled chart are real. Logic tells us. Mathematics tells us. Then there are repeated confirmations between the systems of mathematics and our physically-measured realities. The first 64 notations are foundational and require much more study. The first few notations are initially displayed when one opens the chart online. If one were to scroll through the chart (yes, horizontally scrolled), especially observe how those first 64 notations begin to yield an impressive mass and charge. At just the 64th notation, the Planck Mass multiple is now 4.01495×1011 kilograms and Planck Charge multiple is 34.5986 Coulombs. Yet, the Planck Length and Planck Time multiple are still infinitesimally small. The first actual “measurements” of a multiple of the Planck Length appear to be between Notations 64 and 67; and until recently, the smallest measurement of a fractional unit of time was within the 84th notation.
A rather naive-and-startling conclusion for many, yet seemingly quite obvious, is that the first 60± notations define dark energy and dark matter. It is simple, all-natural, and logically follows. On further analysis, each notation and each doubling is defined by “filling” that notation with the same infinitesimal spheres created within the first notations
The Process: Again, to derive the 202 steps or notations from the Planck base units to the approximate age and size of the Universe today, multiply the four Planck base units by 2 (and the results by 2, over and over again). Perhaps the simplest line to follow is the Planck Time as it doubles up to and beyond the current age of the universe within Notation 202.
The challenge: Now, particularly watch lines 5 and 6 within our large horizontally-scrolled chart: https://81018.com/chart/ We start with Planck Mass (2.176.470×10-8 kilograms) and Planck Charge (1.875×10-18 Coulombs). And it bears repeating — at the 64th doubling or notation, the time and length measurements are still below our abilities to measure directly, yet Planck Mass has increased to 4.01495×1011 kilograms (400 billion kilograms) and Planck Charge has increased to 34.59863 Coulombs (perhaps the inverse processes of a neutron star yet of similar densities). It is assumed that our infinitesimal universe is now heavily-laden with what we call planckspheres, or primordial spheres or first particles. Whatever the name, these are constantly being generated from Notation-0-to-1.
That stretches credulity, then it all goes extreme.
Just beyond the first second of the universe at 1.2023 seconds at the 144th notation, the other values have exponentially increased to 4.8537×1034 kilograms and 4.1827×1025 coulombs. Today we are within the 202nd notation and the Planck time doubling now approximates the age of the universe and the Planck Length doubling approximates the size of the universe. Planck Mass approximates the total mass of the universe and Planck Charge approximates the total coulombs value of the universe. Some percentage of those totals are below our thresholds for measurement, and so, yes, one might conclude, “Here is our ever-so-illusive dark energy and dark matter.”
To review our very first article about this conclusion, go to: https://81018.com/dark/
_________
#4 Start with the most simple and build. Complexity comes quickly.
Redefine the infinite and the infinitesimal: Start with the equation for π.

The finite-infinite relation.4 We will continue studying the role of dimensionless concepts like π (pi). We hypothesize that the qualities that define fundamental physical constants and the dimensionless constants (ratios) will inform a perspective that will help to define the infinite (infinity) as well as the infinitesimal. This definition will not satisfy those scholars engaged in the current debates about the definition and use of infinity within our cultures, yet the hope is that it opens a few possibilities for new discussions. In our little equation (right) C is the circumference of a circle, d is the diameter.
The most-simple, most-ubiquitous, never-ending, never-repeating ratio, pi, is a starting point. By definition, it (1) defines and redefines the infinite, (2) it opens a definition of a finite-infinite bridge, and (3) it opens a range of quantities (and qualities) that capture the infinitesimal across as many as 64 notations.
The abiding concepts that flow within the finite-infinite relation and throughout pi are continuity (order), symmetry (relations) and harmony (dynamics). Yet, these three concepts are also the backbone of the finite, particularly our sciences, the finite-infinite-bridge, and the infinitesimal. Yes, our starting point is — it all started — with π (pi) and then her circle and sphere.4
For an earlier analysis, go to: https://81018.com/introduction
And also, see: https://81018.com/symmetry https://81018.com/harmony/ https://81018.com/π/
_________
#5 Follow the math and the simplest logic.
Mathematically confirm the speed of light:
Follow the numbers.
Light.5 Based on just the accuracy of the determination of the values of Planck Time and Planck Length, the speed of light can be confirmed mathematically. At one second, the Planck Time value is 1 and Planck Length is the distance light travels in one second. The experimentally-defined speed of light is 299,792,458 m/s in a vacuum. Outside the vacuum, it is a variable. Mathematically, it is also a variable. Our current calculation is: 299,792,437.99 meters/second.

Of course, it is not at all surprising that the Planck Time, Planck Length, and the speed of light correlate throughout the chart given that both Planck Time and Planck Length are defined by the speed of light.
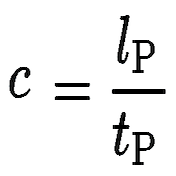
What is surprising is that this simple formula begins to corroborate the basic integrity of the chart and base-2 exponentiation, and it all begs for a much deeper analysis.
For earlier analyses, go to: https://81018.com/formula1/ https://81018.com/c/
Yes, the speed of light is approximated at every notation. It generally ranges around ± .1% of the laboratory defined speed, 299,792,458 meters/second. Just .1% of that value is 299,792 m/s; our current calculations create a range of approximately 213,648 m/s. With our current figures, the highest calculation is 299,982,157 (Notation #16) and the lowest (Notation #3) is 299,768,509.931 (a range of 213,648 m/s). So, Planck’s little equation for Planck Time, Planck Length (lP) divided by the speed of light, c, equals Planck Time (tP), seems to be telling us an important story throughout all 202 notations. Of course, more analysis is required.
Work on these charts began in 2011. To review, go to: https://81018.com/chart/ https://81018.com/home/
_________
#6 Force fit what you can.
Compare their intellectual expansion to our mathematical expansion:
The numbers are the numbers; logic is logic.
Big Bang Subsumed Within Quiet Expansion.6 There is a concrescence between the events of the current big bang theory and our mathematically-defined Quiet Expansion. This analysis opens many questions based on the fact that observational data from the intellectual definition of the Big Bang actually works within the mathematically-defined inflation of our “Quiet Expansion.”
Editor’s note regarding the Quiet Expansion: 20-to-20,000 Hz is the generally accepted range of audible frequencies for human hearing; these convert to wavelengths of 1.7 centimeters to around 17 meters or from the 109th to the 120th notation.
For a direct comparison and earlier review, go to: https://81018.com/calculations
#7 Analyze the logic.
Examine six samples from across the 202 notations or doublings.
Stretch.
The Logic of Numbers.7 To grasp each parameter that defines this chart is not trivial. It requires transitioning beyond our commonsense boundaries. Thinking of the universe as exponential at its core is difficult. Thinking about time as an interval without a past but as encoded as a necessary effect within the entire universe even stretches our sense of relationality. I suspect it will do the same for you. The net-net of studying the simple doubling formula is an entirely different orientation to our little universe of just 202 notations.
Studying the logic of these six samplings does not make it much easier.
For review, go to: https://81018.com/planck_universe/ and https://81018.com/planck-scale/ Also, if you have not looked at the chart of numbers, please do: https://81018.com/chart/
_________
#8 The first sphere.
Sphere stacking is at the heart of all doublings:
Study this most pivotal image.
Stacking/Doubling.8 This simple dynamic image has no less than four key stories. The first story is the emergence of that very first sphere. Sphere stacking is the next story.
The Planck scale, if compared to the atom, is like the atom compared to our solar system. Out of the 202 doublings, 1 to 80, goes from the Planck scale to the atom, and 81 to 160 goes from the atom to the solar system. Surmised is that these planckspheres which have a very small mass and charge, and the smallest length and smallest duration, literally fill the universe (See #3).
That first sphere. It is, by definition, the most simple dynamic of the universe. Yet, there is nothing simple or singular about it. The next sphere comes, and then the next. The centerpoints all connect. That’s an active equation. Stacking has begun. More centerpoints connect. The first sphere interacts with all other spheres, centerpoint to centerpoints to centerpoints.
The story is being demonstrated with the dynamic image (above right) whereby geometries are created. Vertices or nodes, lines, triangles, tetrahedrons and octahedrons literally tile and tessellate the universe as it emerges.
Aether. Many physicists continue to work to justify the concept of an aether. Johannes Kepler, with his work, Harmonices Mundi, now over 400 years ago, had a primitive aether using basic geometries. Kepler then gave us clues with his study of the stacking of cannonballs; and with this image just above. A case could be made for the classic Michelson-Morely 1887 work which looked for a carrier of light waves. When brought down to the Planck scale, the dynamics of the first infinitesimal spheres tell a new story and a very different concept of the aether is introduced.
For an earlier review, go to: https://81018.com/stacking/
_________
#9 Open up period doubling bifurcation.
Get to know this equation:
δ = 4.669 201 609 102 990 671 853 203 821 578
Period doubling Bifurcation.9 In 1975 mathematician, Mitchell Feigenbaum, discovered a limiting ratio for each bifurcation interval. It was a constant. The plain-vanilla version of period doubling was guided by such constants, yet, from my initial studies, nobody could discern why. Nobody was looking at the 202 notations, so certainly nobody was looking below that 64th notation.
There is nothing simple about Henri Poincaré and his work. Yet, when seen from the Planck scale and through the most simple-but-dynamic sphere, an aether that Poincaré may have well envisioned (p.7, The Foundations of Science: Science and Hypothesis…, Science Press, 1913 by H. Poincare, authorized translation by George Bruce Halsted) appears to manifest.
Jules Henri Poincaré. Current studies include applying his conceptual framework for the Poincaré sphere so to open discussions about polarization and its applicability within the dynamics of the Fourier transform. Ostensibly all these dynamics, including Fourier A and Fourier B (below) are part of Notation #1.
That first infinitesimal sphere brings with it a huge agenda, but a deeper analysis of period doubling has been blocked by big bang cosmology.
Here, perhaps, we can begin to discern the mathematics and geometries that are the basis of period doublings bifurcations. Of course, we’ll continue looking at sphere stacking. We’re learning how to dance in this sphere of influence. Still entirely clumsy, there is a lot to learn.
In a recent article, I said, “...now included are Mandelbrot’s work on fractals, the Santa Fe Institute and their work on complexity and chaos theory, and Stephen Wolfram on computational irreducibility. In 2006 Ari Lehto refocused his work to explore period doubling at the Planck scale and in 2014 Charles Tresser added insights regarding its universality.” https://81018.com/transformation/
For more, go to: https://81018.com/transformation/#9b and https://81018.com/e8/
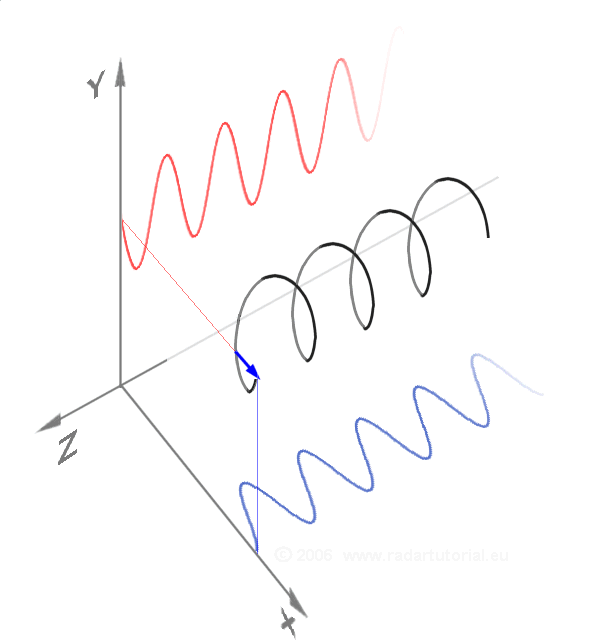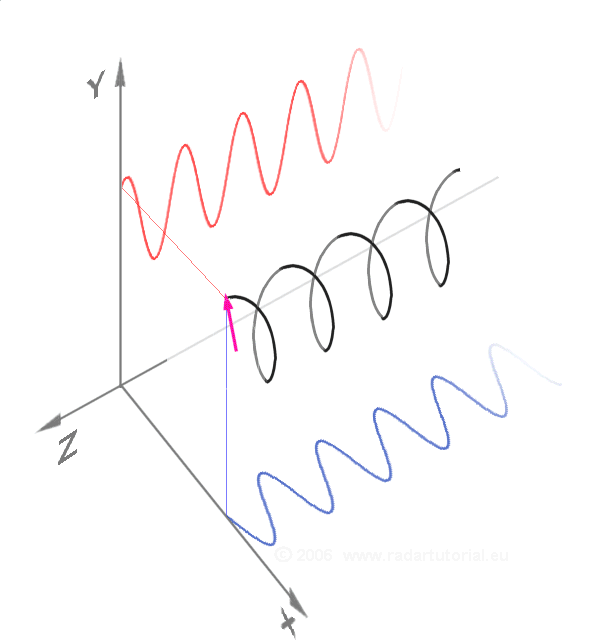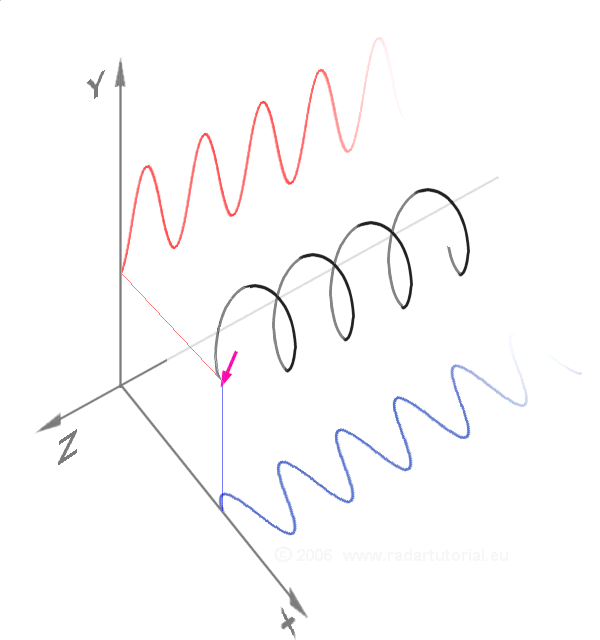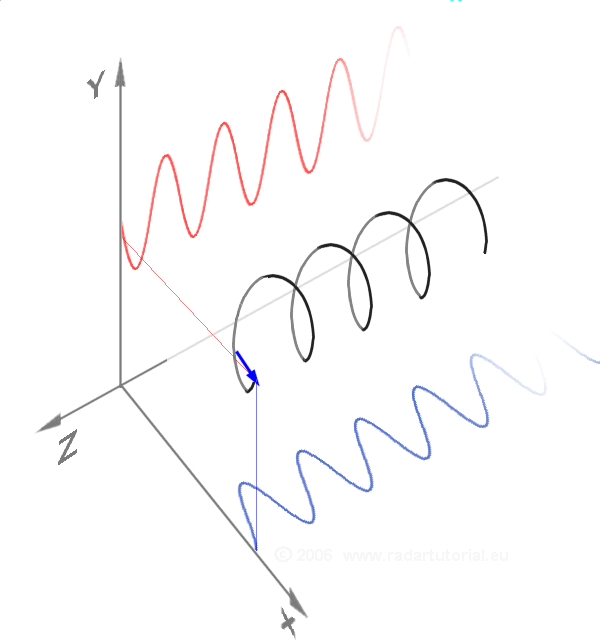
#10 Test the Fourier series.
Begin an analysis of the dynamics at the primordial scale (i.e. the Planck scale).
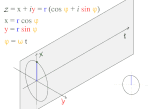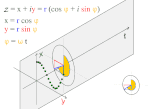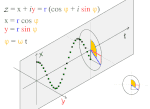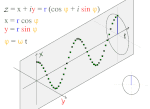
Fourier Transform.10 There are so many equations within the Fourier transform, it rather quickly spins one’s head with calculations. Where period doubling captures the moment when things become two, here we discover how two things are dynamically related to all other things. The Fourier transform has such a diversity of applications, it touches every part of our life. Yet, to the best of our knowledge, at no time has its inherent power been explored at the Planck scale. It, too, has been hidden by big bang cosmology.

Fourier B
It appears that the Fourier transform at the Planck scale could open a new discussion of the very nature of “gravitational weak” and “electromagnetic and strong.” Just observe the two graphics on the right. Click on each image to go further.
More coming from equations of motion, structural dynamics…
For review, go to: https://81018.com/transformation/#10b
_________
#11 This is where it is all going.
We’re living in an exponential universe and among all things infinite:
We’ll all continue studying Euler’s equations.
Euler.11 Our chart and all these formulations are inherent within an application of Euler’s exponentiation. It assumes a Planck-scale sphere, herein called a plancksphere, which has been populating the universe from the first instance of space and time, and, it creates a basis for a mathematical physics, a new foundational science that gives rise to particles and waves.
Euler’s formula, named after Leonhard Euler, is a mathematical formula that establishes the fundamental relationship between our most basic and our more complex mathematics.
If the universe is fundamentally exponential, it changes the paradigm. It is a very different foundation. If space and time are derivative and finite, this model becomes a major transition. There are basic concepts to be re-instantiated. And, over the past 40 years, there are many very confident articles, books, videos and movies that will need to be updated and rewritten, and a whole new universe needs to be explored.
For review, go to: https://81018.com/pursuit/
_________
#12 Geometries of probabilities and fluctuations.
Study the geometries of gaps:
Indeterminacy is geometrical.
Logic is logic. A gap is a gap.12 This model of the universe brings pure mathematics into the picture within the first notations. Everything is used and needed — algebra, calculus, geometry and topology, combinatorics, logic, and number theory. Then, by the 64th notation much of the applied mathematics is required, especially dynamical systems and differential equations, mathematical physics, information theory (and, yes, even signal processing).
Within this particular article, we have not discussed the application of probabilities-and-statistics and game theory. These studies are also put to the test. At some notation (or notations) within the scale from 1-to-64, a simple geometry of probabilities is introduced. That geometry has been discussed in many documents on this website. Even before we had our first Big Board, we were discussing squishy geometry in our high school. It all begins with just five tetrahedrons (seven nodes), but includes the icosahedron, and then the Pentakis dodecahedron. That gap is real and ubiquitous within basic geometries.
- https://81018.com/number/#Pentastar
- https://81018.com/fluctuations/
- https://81018.com/geometry/
- https://81018.com/geometries/
- https://81018.com/notations/
Conclusion.
This article is just a start. Yes, it’s part of an eight-year start! The work is still in the earliest possible stage of exploration. -BEC
* Yes, a little like an old-fashioned 12-step program: Here for those who need a little help to break free of big bang cosmology (it has been so profoundly ingrained and is totally addictive), yet, be cautioned, this is a first draft! Another draft is here.
_____
1 What is a second? Technically within the International Organization for Standardization (ISO standards) the second is one of seven SI base units. They define a second as “9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom.”
There is nothing intuitive or simple about it and we believe there is a more intuitive way.
In light of the entire universe. By using the chart of 202 base-2 notations, we actually start at the Planck scale and go to the current time. Here a second is easily defined in light of the entire universe. Based on a a multiple of Planck Time, one second is between Notations 143 (just .60116 seconds) and Notation 144 (where the doubling is now 1.2023 seconds). This second is defined by dimensionless constants that are universal, not by physical measurements done by people and machines.
Could these Planck units provide a basis for standards? To attempt to open up that question for dialogue, we will engage many of the people throughout the International Organization for Standardization (ISO). We have asked Dr. Ian Robinson of the UK’s National Physical Laboratory. We have also asked scientist/scholars at the National Institute for Standards & Technology here in the USA. Can we get beyond the “local measurements” of the instruments like those done by the Wilkinson Microwave Anisotropy Probe (WMAP), the Hubble Space Telescope, ESA Planck satellite, and NASA’s Spitzer Space Telescope? Perhaps all forms of measurement with devices, instruments, and tools should be to confirm not to determine a standard.
When the second is defined in light of Planck Time, the entire chart will come alive for many more people.
[1g] In 2012 we first suggested a concept like it, “Use the Planck Length to define a meter.” A NASA scientist who was helping us with some of our calculations thought it was a worthy idea. Defining the number of seconds in a year should be trivial and not quite so tortured!
The dilemma. Almost everyone in this world believes that space and time are absolute. That concept is part of the fabric of our commonsense. To think of time as the Now, where the universe is constantly changing and evolving in part based on what is happening Now, flies in the face of that commonsense. That the universe is always the total sum of all its relations, an actual composite of all relations everywhere for all time, is just too big for most of us. A little like Kermit, a frog singing his song, “It’s not that easy being green,” it is also not easy to change our orientation.
2 202 doublings of the Planck base units. The Planck units have had a slow ascendancy. In December 2011 when we backed into our model of 202 base-2 notations, we were chasing simple embedded Euclidean geometries (tetrahedron and octahedrons). It had structure, logic, simplicity, and energy (light and coulombs). It was comprehensive and predictive, but it flew in the face of (1) Isaac Newton’s absolute space and time and (2) big bang cosmology. Both have had sharp and well-informed critics over time, so it seemed a natural coalition to build on their arguments. Also, it appeared that the cost-benefit analyses weighed in our favor. It was therefore “just” a matter of making the case for it, building a consensus, and then a group of advocates with as many possible people and within as many disciplines as possible.
May the circle be unbroken. In September 2019, the the television producer, Ken Burns, released a block of shows about the history of Country Music. The sixth episode featured an iconic, highly-symbolic country song about unbroken circles; our focus turned to pi and the infinite.
In the original 1907 Ada R. Habershon version, the question was asked, “Will the circle be unbroken?” The 1935 Carter Family version asks, “Can the circle be unbroken?” We proclaim, “May the circle be unbroken.” It is not a question. Human circles are always broken, physical circles tend to be imperfect. Yet at the deepest levels (Notation #1), conceptually these circles are never broken and give rise to the laws of conservation of energy and matter.
The mystery of pi. A ratio, never-ending, never-repeating, always a relation, it stretches well beyond us, and it is ubiquitous. It doesn’t have space-time coordinates but is part of all space-time coordinates. While dancing around a new definition of the infinite, I say, “Let pi be our initial definition of the infinite and infinity. Forget all other definitions.” If we start with pi, we can let pi inform any and all more complex definitions. So, within this context, we considered potential infinite qualities. Today, these are continuity/order, symmetry/relations, harmony/dynamics. There is also the randomness and uniqueness within the “never-repeating” aspect of the ratio. What else? I could not grasp more so turned to the scholars and scientists who have made pi their primary study.
So, there should be more to come, yet those concepts of professional scholars and scientists could also be spread out in the endnotes, footnotes, references and resources…
3 Dark Energy & Dark Matter. This work is not theoretical. It is mathematical. It is practical. It is logical. It really is a new order of commonsense that asks everyone to reconsider the very nature of their own logic. It is a simple chart that easily defines dark energy and dark matter. Yet, it is also non-intuitive. Time has a new face. Infinity has a key role. Base-2 exponentiation, a doubling mechanism, burst out of the most simple geometries which burst out of a stacking of spheres. The whole chart of 202 notations became a working model of the universe because it is so very simple. And, there is no extralogic to carry it forward. And, yes, although the Planck units were overlooked for many years, that is not the case today.
Possibly more to come…
4 Redefine the infinite and the infinitesimal. Throughout history, the finite-infinite debate is fraught with emotion with those who “believe” and those who do not. Those debates are ignored. We attempt to start with a clean slate — tabula rasa — by starting with most simple concepts that defy a finite label to the most advanced, the current work within renormalization and regularization whereby infinities are carefully analyzed so to control that influence. Here are perhaps are the most advance concepts about infinity and infinitesimals. Also, the highly-technical descriptions of infinity and the infinitesimals by out most erudite scholars have yielded concepts with highly-specialized language. That work will be engaged, but always with a goal of discovering new relations that could be used to influence the general perceptions of the world’s people.
To start simply and modestly, the qualities of pi were analyzed.
Within classic studies of the electron, the electron is a point particle with a point charge and no spatial extent. The radius formula is:
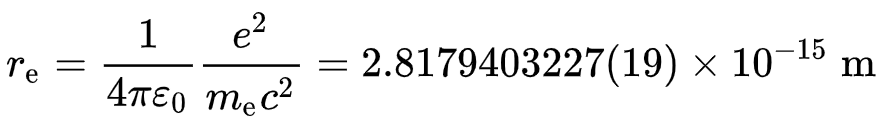
Within our base-2 chart, this “point” particle falls within Notation 60. There are 60 doublings of the Planck scale prior to reaching the size of a “point” particle. Denying this infinitesimal range seems a bit too sure that particles and waves are our fundamental building blocks with which to construct our universe. As we shall see within the remaining key concepts of this article, the simple sphere, once it begins stacking, is simple no longer.
See: https://81018.com/infinity/
More to come… Question: What is an “infinity moment”?
5 Light: Time, Length, Mass and Charge Two of the most simple-and-basic formulas open a key discussion. Reviewing line 10 of the horizontally-scrolled chart is the simple division of each Planck Length multiple by its associated Planck Time multiple for all 202 notations. We discover that the result is very close — within .1 % of the laboratory-defined speed of light in a vacuum: 299,792,458 meters per second. Space and time are the first-order equivalence of light and they are a Janus face. Einstein’s oft-quoted formulation is a second-order equivalence whereby, with the speed of light squared, mass and energy become a Janus face.
And, yes, line 10 of the chart is the first simple confirmation that model has some cogency.
There should be a bit more to come…
__________________
6 Big Bang easily swallowed by a Quiet Expansion. The big bang’s isolation is absorbed within the logic of our natural inflation. Guth, Linde et al have been hit long and hard enough about the extraordinary measures taken to hone that old theory. The 1999 University of Cambridge, Newton Institute conference, Structure Formation in the Universe (the book), may have set the foundation for a major revision, yet something as simple as the base-2 chart, perhaps Wheeler’s Dream, is apparently just too simple for many.
____________________
7 Logic 101: The chart has too much information to analyze quickly, but the simple logic tells us that the universe is exponential. It tells us that there is an infinitesimal universe that is ordered, has a geometry, and has at least 60 domains, 10-34 meters to 10-18 and 10-44 to 10-26 seconds, each increased by doubling (base- 2) each step of the way.
Of the many people with whom I have spoken about this work, a biology professor, George Fox, asked for some clarity. Dr. Fox is a leading biologist who has had firsthand experience introducing new concepts. He asked me to examine the logic of samplings across the 202 column grid and this 2016 article resulted. New concepts take time and often go through a fair amount of deprecation before being accepted.
Examining that logic was challenging. Yet, because we believed we were engaging a new model of the universe, a new concept of time-and-space and charge-and-mass, we have been patient with the challenge and with our own gaps in knowledge. What we did learn was that although it stretched our understanding of logic, it was not illogical or extralogical.
Notations #1 to #64: The challenge now is to build a mathematical foundation for the universe that starts with spheres, the deepest dynamics inherent within all spheres at the Planck scale, and to date, we are examining the structuring within cubic close packing, period doubling bifurcation, and the Fourier transform. Eventually, we will attempt to bring in the more classic studies of holonomy and conformal field theory as well attempt to build a mathematical-and-natural progression to particles and waves.
Along this path whenever possible, dimensionless physical constants and fundamental physical constants will be applied. Dimensional analysis and Buckingham π theorem will be employed. The concepts of nondimensionalization and natural units will be further analyzed until this new system of measurement begins to make sense to others.
Planck units use the gravitational constant G (a constant of proportionality) measured in a laboratory to just four digits. The modern notation of Newton’s law involving G was introduced in the 1890s by C. V. Boys. The first implicit measurement with an accuracy within about 1% is attributed to Henry Cavendish in a 1798 experiment.
____________________
8 Sphere Stacking: A Fundamental Dynamic Of The Universe. Three necessary facets of physicality:
- One plancksphere created the initial bridge.
- Endless planckspheres are being generated from Notation #1; this is the expansion.
- Sphere stacking (doublings) define all subsequent notations.
- Nodes or vertices, lines, triangles, tetrahedrons, and octahedrons begin their definitions within the first ten notations, and thereafter become projective and Euclidean geometries.
What began as a centuries old problem to maximize one’s the use of space was then applied to crystal and atomic structure, and now it goes ever so much smaller into the Planck scale.
Cubic close sphere packing began around Notation 114; it was then applied chemical structure and went down into the notations around 90. Then it was applied to atomic structure and went down into notations around 80. With this next application, we bring it all the way down into Notation #1.
____________________
9 Period doubling bifurcation. We are trying to discern if anybody has defined a mechanism that could explain a period doubling hierarchy. Though studied as early as 1887 by Lord Rayleigh, it appears to be somewhat of a mystery. I’ll check with Ari Lehto, Charles Tresser and some of the other scholar-experts to find out where the edge of that research is today.
So, of course, there is much more to come…
____________________
10 Fourier series, transform: The goal here is to bring everyday physics and mathematics to bear to grasp the foundations of our universe so there is nothing esoteric or extra-logical about it. How very satisfying it will be if key mathematicians throughout our history, people like J. Kepler-C.F.Gauss-T.C. Hales (cubic-close packing), Poincaré-Feigenbam (period doubling bifurcation), and Fourier-Dirac-Strogatz (Fourier transform), are responsible for the concepts that describe and predict the behaviors of our infinitesimal universe.
To that end, we are going over these details just one more time. I know we are missing a lot.
So, of course, there is much more to come…
____________________
11 Euler’s Equations: The most beautiful equation, Euler’s identity, will have a key role in this model. I am not sure how and who yet, but some mathematical genius, somebody like Po-Shen Loh (video), will come along and tell us. Exponential notations, 22, 23 and 264 and 2202 are all key steps for our students to begin to grasp the so-called “singularity” and harmony of our universe.
Again, of course, there is much more to come…
____________________
12 The place and power of simple logic: Where there is continuity, there is discontinuity. Where there is symmetry, there is also asymmetry. And, where there is harmony, there is dissonance-and-the discordant. If the infinite is ever to be meaningful for science, the historic definitions of infinity from philosophical and religious thinkers should be ignored. Defining the infinite as continuity, symmetry, and harmony allows infinity to penetrate the finite and we need not be concerned with Hilbert’s consternation about the exclusivity of each from each other. There is a transformation between the two and it is believed that a finite-infinite bridge can be defined much more clearly.
So, of course, there is much more to come…
Research, references and resources:
“Planck Second” between Notations 143 and 144:
- https://journals.aps.org/rmp/abstract/10.1103/RevModPhys.88.035009
- https://codata.org/blog/category/si-redefinition/
- The CODATA 2014 values of h, e, k, and NA for the revision of the SI by D B Newell, F Cabiati, J Fischer, K Fujii, S G Karshenboim, H S Margolis, E de Mirandés, P J Mohr, F Nez, K Pachucki, T J Quinn, B N Taylor, M Wang, B M Wood and Z Zhang.
- http://www.codata.org/committees-and-groups/fundamental-physical-constants
- CODATA Task Group on Fundamental Constants: F. Cabiati, Istituto Nazionale di Ricerca Metrologica, Italy; J. Fischer, Physikalisch-Technische Bundesanstalt, Germany; K. Fujii, National Metrology Institute of Japan, Japan; Savely G. Karshenboim, Pulkovo Observatory, Russian Federation and Max-Planck-Institut für Quantenoptik, Germany; E. de Mirandés, Bureau international des poids et mesures; P. J. Mohr, National Institute of Standards and Technology, United States of America; D. B. Newell, National Institute of Standards and Technology, United States of America; F. Nez, Laboratoire Kastler-Brossel, France; K. Pachucki, University of Warsaw, Poland; T. J. Quinn, Bureau international des poids et mesures; C. Thomas, Bureau international des poids et mesures; B. N. Taylor, National Institute of Standards and Technology, United States of America; B. M. Wood, National Research Council, Canada; and Z. Zhang, National Institute of Metrology, People’s Republic of China.
Base-2 Exponential Notation
- Why Trust A Theory? from a conference, Reconsidering Scientific Methodology in Light of Modern Physics, 7-9 December, 2015
- Study algebraic phenomena inhabiting the murky boundary between finite and infinite with Alexandre Borovik
- Study the tension between intuitive infinitesimals and formal mathematical analysis with Mikhail G. Katz (and David Tall)
- Crossroads in the History of Mathematics and Mathematics Education edited by Bharath Sriraman, University of Montana
- Wendy Freedman, University of Chicago, once director of the Carnegie Observatories in Pasadena, California, and an expert on the Cepheid variable whereby a star pulsates radially, varying in both diameter and temperature and producing changes in brightness with a well-defined stable period and amplitude.
- Lewis Carroll‘s The Mad Gardener’s Song includes the lines “He thought he saw a Garden-Door / That opened with a key: / He looked again, and found it was / A double Rule of Three“[7]
Quantum Electrodynamics and Planck-Scale, Rainer Collier, 28 Sep 2017 arXiv:1710.00618v Institute of Theoretical Physics, Friedrich-Schiller-Universität Jena, Max-Wien-Platz 1, 07743 Jena, Germany
Dark energy and dark matter
Infinity, infinitesimals, dimensionless physical constants, hierarchy problem
- A smooth function which is nowhere real analytic
- Instanton
- Peter Mohr WidmaierMohr@t-online.de Cross sections at sub-Coulomb energies
- homotopy group of SU(2)
- topological vacua
- abelian gauge group
- Yang–Mills theory
- BPST instanton after its discoverers
- Alexander Belavin
- Alexander Polyakov
- Albert S. Schwarz
- Yu. S. Tyupkin
- pure gauge at spatial infinity
- nonrenormalization theorems
- perturbation theory
- Equations of motion are grouped under three main types of motion:
- translations, rotations, oscillations
- Robin Cope Hartshorne (Berkeley):
- The idea of T-duality was first noted by Bala Sathiapalan in an obscure paper in 1987[1].
Wikipedia’s dimensionless qualities
- Newtonian constant of gravitation
- Newtonian constant of gravitation over h-bar c
- Planck constant
- Planck constant in eV/Hz
- Planck length
- Planck mass On 20 May 2019, World Metrology Day, the world said goodbye to the original kilogram as the redefinition of the SI base units come into force.
- Planck mass energy equivalent in GeV
- Planck temperature
- Planck time
- reduced Planck constant
- reduced Planck constant in eV s
- reduced Planck constant times c in MeV fm
- speed of light in vacuum
- vacuum electric permittivity
- vacuum magnetic permeabilityy
- http://www.fields.utoronto.ca/people-and-contacts
- Newtonian constant of gravitation
Period doubling bifurcation
- …a fine string is maintained in transverse vibration by connecting one of its extremities with the vibrating prong of a massive tuning-fork, the direction of motion of the point of attachment being parallel to the length of the string …the string may settle down into a state of permanent and vigorous vibration whose period is double that of the point of attachment.
- Nonlinear dynamics: chaos are period doubling… intermittency, horseshoes and homoclinic orbits.
- chaos is always regarded as intrinsic randomicity of determinate dynamical systems.
- …attractor undergoes a period–doubling bifurcation which converts it from a period-1 to a period-2 attractor. This bifurcation is indicated by the forking of the curve
- The
 -coordinate of the Poincaré section of a time-asymptotic orbit plotted against the quality-factor
-coordinate of the Poincaré section of a time-asymptotic orbit plotted against the quality-factor  .
. - Poincairé (1) bifurcation theory (1885), The Future of Mathematics (PDF) (Weil) (Wikipedia), Sphere, Homology Sphere (Evelyn Lamb, 2017)
- On the scaling structure for period doubling (PDF), Garrett Birkhoff, Marco Martens & Charles Tresser, Astérisque, Société mathématique de France, 286 (2003), p. 167-186
- Connecting period-doubling cascades to chaos, Evelyn Sander, James A. Yorke, 17 Feb 2010
- ventricular fibrillation (VF) is an application of period doubling
Fourier transform transforms
- Fourier, Quantum Electrodynamics and Planck-Scale,
Rainer Collier, 28 Sep 2017 arXiv:1710.00618v, Institute of Theoretical Physics, Friedrich-Schiller-Universität Jena, Max-Wien-Platz 1, 07743 Jena, Germany
- Fourier, Quantum Electrodynamics and Planck-Scale,
Euler exponentiation
- Euler, https://www.youtube.com/watch?v=IUTGFQpKaPU Yet, we ask, what are these people thinking when they voted for these equations:
- The Dirac equation. 27,061 votes. 34%
- Euler’s identity. 13,745 votes. 17%
- Pi. 9,937 votes. 13%
- The wave equation. 3,761 votes. 5%
- Riemann’s formula. 4,271 votes. 5%
- The Euler-Lagrange equation. 3,176 votes. 4%
- The Yang-Baxter equation. 1,592 votes. 2%
- Bayes’s theorem. 2,958 votes. 4%
- Euler, https://www.youtube.com/watch?v=IUTGFQpKaPU Yet, we ask, what are these people thinking when they voted for these equations:
The logic of quantum indeterminacy
- https://en.wikipedia.org/wiki/euler
- https://en.wikipedia.org/wiki/Lists_of_mathematics_topics
- Doubly Special Relativity theory (DSR), loop quantum gravitation, the introduction of non-commutative geometries, the use of specially deformed Lorentz algebras, as well as several generalized uncertainty principles (GUP) in which the Planck momentum occurs.
Planck Length compared to the atom is like the atom compared to the Solar System. We have a lot to learn about the infinitesimal!
Initiated in private on September 5, 2019
Protected posting: Thursday, September 12, 2019
A first draft homepage: Monday, September 30, 2019
Most active editing: September 9 to October 5, 2019
Most recent update: 25 March 2022
Please visit the most current article on the home today.
If you appreciate what we are doing here, please “like” and “share” this page. Thank you.