Pi Day, March 14, helps to focus on the meaning of pi (π ).

CENTER FOR PERFECTION STUDIES: CONTINUITY•SYMMETRY•HARMONY•USA•GOALS•March 2019
HOMEPAGES: ASSUMPTIONS|DARK|EMERGENCE|INTRO|INFINITY|MAX|ORIGINAL|REVIEW|Scholars|WEINBERG
Pi

Pi: Fundamental To Everything

by Bruce E. Camber   Pi-Day Celebrations   It’s Perfect

One of our goals is to help us all think about pi in new ways. There is a surprising amount of original work 1 around our never-ending, never-repeating, always-the-same, π (pi). We all can learn something new about pi. After all, it is our most important dimensionless constant, arguably the most-used ratio (equation) in the universe. For example, Steven Strogatz, a mathematics professor at Cornell, wrote Why Pi Matters for The New Yorker for March 13, 2015. That article pushed me right back into 1961, my earliest explorations of geometry and physics. He pushed me to think about pi in new ways. Fourier’s work came alive for the first time.2

I opened an email from my friends at MIT’s OCW or OpenCourseWare,3  “Counting down to Pi Day.” It was signed by Krishna Rajagopal, a distinguished physics professor and now also the Dean for Digital Learning:

Re: Counting down to Pi Day (π )

Dear Bruce,

March 14 is a big day for MIT. It’s Pi Day, the annual celebration of the mathematical constant π, (and you know how we feel about math). It’s the day MIT shares its admissions decisions every year for the incoming undergraduate class. And, for the past two years, it’s been MIT’s global day of giving to support the Institute.

At OCW, we’ve surpassed our Pi Day goal the past two years because of generous supporters like you who believe in our mission of transforming education through open access…

(And he goes on…)

I thought to myself, “Everybody is always looking for money. We need to be looking for more meaning. We should be digging more deeply into the very nature of pi.”

The more we know, the more we grow.
The more we know, the more there is to know.
So, I immediately wrote back:

Dear Dean Prof. Dr. Krishna Rajagopal:

Let’s make Pi Day a real pi day.Let’s quiz the student body:
1. Where does pi come into play within the big bang?
2. How does pi affect wormholes and blackholes?
3. What does pi do at the Planck scale units of length, time, mass and charge?
4. What role does pi play in defining all our dimensionless constants?
5. Is pi the essence of a finite-infinite bridge?
6. Are pi’s never-ending, never-repeating numbers the essence of infinity?

Pi Day Cheesecake from 7ate9 Bakery

I am sure there are millions more important questions about pi that your student body could ask and should answer. My little sampling just above is off the cuff.

So first, we’ll need to get the best possible questions listed. Let’s post those as an on-going challenge to the student body with a system of one person – one vote. All questions are initially posted. The ones with the highest votes rise to the top. The ones with the most negative votes are deleted.

Each year any new answers to each question are posted; and again, one person-one vote, the best rise to the top. We could annually reward the five best questions and the five best answers.

That would be two contests:
1. Who can come up with the best questions to get into the core values of pi? We can get started as soon as somebody writes that code for your website.
2. Then, who can come up with the best answers to the best questions about pi?

The winners would each receive their choice of a pie from one those shops that were voted Best of Boston & Cambridge (the seven links just below open a new page to the sweets.

It should fly! And, we will annually learn a little more about pi!
-Bruce

PS. I’ll sponsor the pie for a few years if you’ll get all that code working! -BEC

Yes, on this Pi Day 2019, let us all try to go deeper, beyond what we have already learned about pi (π ). You can do it.

###

Endnotes, Footnotes, References & Resources

1 Original Work To engage some of the more recent scientific papers about pi simply put Pi + ArXiv in your favorite search engine and you’ll have reading materials for several months! Most of that reading is rather heavy-going. I am plodding through an article by Andreas Maier and Peter Marquard, Life of π. Sounds like it might go in-depth about the attributes of pi, but it is about “…the heavy-quark contribution to the polarisation function Π at higher perturbative orders.” With about 239 references to pi, mostly in formulas, it requires strong knowledge of mathematics and physics. It is a good read just to be reminded about how much we don’t know what we don’t know! Thanks, guys! I will readily attest to eating humble pie every day and almost every hour in this work!

More general references can be found by enter Pi + 2019 yet now you get over a billion references! So, try copying a title that you think might be fun to explore. For example, I enter, Profound Understanding of the Value Pi and the first listed is Steven Strogatz’s New Yorker article discussed in the next footnote!

Our analysis of pi is still rather rudimentary, but at least we are trying:

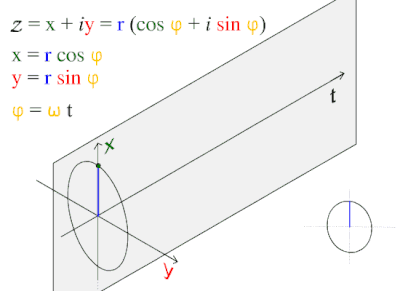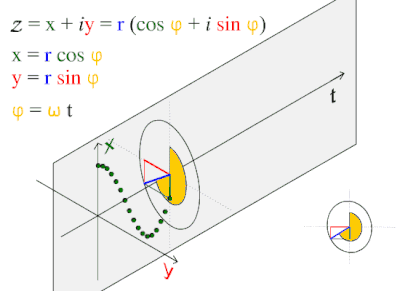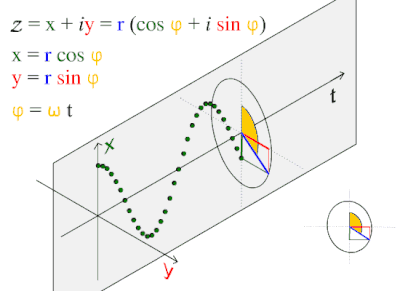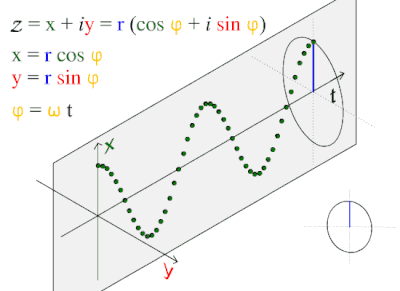
We are trying to incorporate the following three images into the interpretation of the first few notations. Obviously, pi plays a key role in it all:

Sphere to tetrahedron-octahedron couplet

2 Steven Strogatz, Cornell University. The author of Why Pi Matters, The New Yorker, 2015, Prof. Dr. Steven Strogatz opens pi up so we begin to see some of her key inner workings through the work of J-B. J. Fourier (1822) analysis and series. To take his analysis to the Planck scale perhaps renders a more primordial understanding of sine and cosine, and the internal dynamics of the radius to circumference. That possibility should not be minimized. Isn’t the first instance of polarity beginning to shape? Isn’t this where string theory needs to begin? How can we truly discern color, charm, M-theory, superstrings, and vibrations in 10 dimensions unless we can follow a simple chain of command? I propose that string theory will get nowhere until these three simple dynamic functions of pi are included at the beginning (“rather sweetly naive”).

3 MIT’s OCW or OpenCourseWare. Fill in the gaps in your education with any on of 2400 courses. Although there is no introductory course about pi, there is a Session 7, Derivatives of Sine and Cosine, that will open many doors all around pi.

MIT has been an important place in my life. I began work among them in 1971 first as an outsider interested in the work of Jay Forrester / Dennis Meadows and computer modelling. In 1972 physics professor, Phil Morrison, and his wife, Phyllis, became personal friends because we shared similar interests about budgets, the military, and eventually the scale of the universe. A computer-information-physics-philosophy professor, Ed Fredkin, became an acquaintance through a mutual friend, Ted Bastin, when he was my house-guest while visiting Boston. Then, I met Victor Weisskopf, former chairman of the physics department, who helped with my visit to CERN so I could spend time with John Bell. Then, in 1979, I organized a display project on questions about principles. They ushered me up to meet the movers-and-shakers of the Machine-Architecture group (which later became the infrastructure for the Media Lab). And then most recently, I have had the help of physicist, Frank Wilczek, to begin to grasp the Planck scale. MIT has always been been open and encouraging and informative. OCW is MIT; it is carrying on a tradition that is built into the DNA of the school. Over the years, I have been guided by the work of literally dozens of other faculty members as well.

Five assumptions about the nature of the universe

A Construct For A New Orientation

Challenge us. Coach us. We need all the help we can get.

Which concept is strongest? Which is weakest?

###