CENTER FOR PERFECTION STUDIES: CONTINUITY•SYMMETRY•HARMONY GOALS March.2020
PAGES: ASSUME|Basic | DARK |FORMULAS|INFINITY|KEYS| Map | RELATIONS|Transformation|UP

_______________________________________
Determinant becomes undecidable,
uncomputable and unpredictable
_______________________________________

Bruce E. Camber
Big Board-little universe Project: http://81018.com
500 East Fourth Street #484, Austin, TX 78701
camber@bu.edu

April 22, 2020

     Abstract

Apply base-2 exponentiation to the Planck base units and the universe is parsed within 202 notations or doublings. These initial Planck units are derivative and finite. All the values by which each is defined opens questions about the nature of the finite-infinite relation. Within this emerging model, infinity is: 1) continuity creating a finite order and time, 2) symmetry creating finite relations and space, and 3) harmony creating finite dynamics and a space-time moment. No other definition of infinity or the infinite is engaged. Within this construction there is a small range of notations, the dynamics of which are determinant and are also understood to inculcate the following: decidability, computability, and predictability. Then comes a range of domains, the dynamics of which transition to the indeterminate and a transmogrification to undecidability, uncomputability, and unpredictability. There is a domain of perfection with no quantum fluctuations and a much larger domain of imperfection where quantum fluctuations have become dominant.

Keywords: Planck base units, Planck Time, Planck Length, Planck Charge, Planck Mass, base-2 exponential notation, determinant, decidable, computable, predictable, indeterminate, Gödel, undecidability, uncomputability, unpredictability, sphere, sphere stacking, spherical perfection, cubic-close packing of equal spheres, Langlands programs, Witten, string theory…

Introduction. Our simple mathematical outline of the universe was unceremoniously developed and posted on the web in 2011 from within a New Orleans high school. That model has 202 base-2 notations which assumed the first moment of time is Planck Time, and that it goes to the current age of the universe, today, or the Now. Initially considered to be a good STEM tool, it is now believed to be more.

The Focus. We are projecting that within the first 64-notations, just below thresholds of physical measurements, there is a dynamic range of perfectly-defined domains, and then, an even more dynamic range that transitions between determinacy and indeterminacy. These first 64 notations, we believe, are the grounds for the decidable [1], the computable [2], and the predictable [3]. An irony is that although logically determinant, these values are too small to be measured. Once measurable, the measurements become indeterminate. It is a fundamental transmogrification to undecidability [4], uncomputability [5], and unpredictability [6].

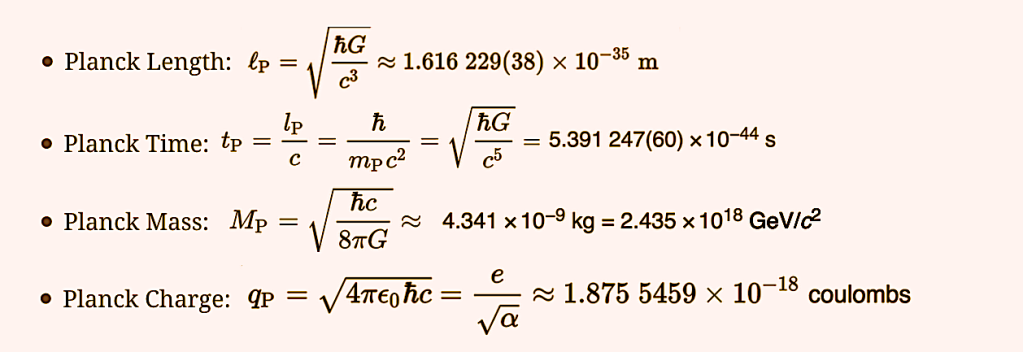
Planck base units. We begin with the Planck base units of time, length, mass and charge. We take these face values as a given and ask the question, “What would the universe look like if the very first moment begins with the instantiation of those four values?” Of course, these values are the result of equations with additional values used by Max Planck to render his four basic numbers.

Consider the four equations and their numbers for space (length), time, mass and charge (Illustration 1).

Background. In our high school geometry classes the question was raised, “If the Planck Length and Planck Time are the smallest possible units of length and time, does it follow that these are also the very first units of length and time? [7] Does it follow that these equations, with all their dimensionless constants, come together to become the very first moment of physicality?” We were unwittingly opening the “CDM of the universe” and wondered if Steven Weinberg would call it a “grand reductionism” [8].

Our postulate is that these Planck’s units are really-real physical entities, not zero-dimensional point particles, but an actual entity defined by those base unit values. So our next question was, “What would this entity look like?”

Every equation is in part defined by the speed of light, pi (π) and the Planck Constant.

Because our students were studying basic geometric structures, they had a few answers. Yet, after some discussion, the students of pi, circles, and spheres prevailed. We then assumed not one sphere, but an impossibly-fast, steady stream of primordial spheres emerge. We then wondered what the next dynamic could be.

We decided to invoke Kepler (1611) and his sphere-stacking exercise of that year. (Illustration 2). So analogically, like Kepler, we now have this infinitesimal, raw stacking of spheres. We consider the first ten notations. Within Notation-10 there could be as many as 256 spheres. However, if we follow the advice of Freeman Dyson regarding scaling vertices and dimensional analysis, there could be as many as 67,108,864. Go to the (Chart, column 10, lines 8 & 9). We decided that at some point we would learn a deeper logic and we would be able to decide.

The dynamics still beg the question, “What happens next?”
 Our students had a quick answer, “The spheres come alive.”

First, there are the dynamics within cubic-close packing of equal spheres. The radii “discover” radii (see Illustration 3), and triangulation begins aka, triangulated coordination shells [9]. The discovery process continues and a tetrahedral layering begins enclosing octahedral cavities.

There are structures within structures.

Fourier [10] rolls in with the initial transform. Then comes Lorentz.[11] with linear transformations. The spheres are tied together and become Poincaré spheres [12].

There is so much to learn here and we’ve only just begun.
The key point is that everything fits perfectly.
Pure geometry meets physics 101.

Spherical perfections. Within this thrust to create perfect continuity, perfect symmetry, and perfect harmony, this infinitesimal universe takes shape. The plancksphere [13] dominates. In theory, there is nothing that is undecided, uncomputed, and unpredictable. It is all a quiet emergence within a simple perfection. It’s creating an isotropic and homogeneous universe. Infinitesimal and way too small to measure, these are domains reached only by logic and mathematics. Actual physical measurements of a length begin around the 67th base-2 notation; and, the first unit of time, the attosecond, is not measured until the 84th notation. Thus, there is an extraordinary amount of intellectual space to tie logic, numbers and geometries together. Of course, it will be a challenge, but it just may be relatively straightforward for some scholars.

It is a study of perfected states in space-and-time.

The Expansion: Geometric, arithmetic, and exponential. Scholars within Langlands programs and string theory have done major work to define this space and its automorphic forms [14]. Here is a discovery process whereby every equation within Langlands programs has a place within a highly-structured environment. Every radius of each sphere (a string) opens Witten’s equations of state and the Seiberg–Witten invariants [15].

This simple base-2 ordering system quickly becomes complex. Each of the nineteen subsequent prime-number notations — 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, and 61 — introduce even more complex mathematics. The remaining prime numbers — 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 197 and 199 — open new physical potentials.

Also, base-2 is just one dynamic of this expansion. This universe appears to be opportunistic so may well use the other prime number bases — base-3, base-5, base-7, base-11, and base-13 (right up on up to base-101 — to introduce yet even more complex functions [15]. Of course, a majority of notations are included within base-3 (67), base-5 (40) and base-7 (28).

Within this model all notations are always active. They build off of each other.

Finite-infinite. This system is its own self-enclosed system, a working finite model theory, with its own rules and axioms that are grounded in a problematic statement — the origins of this perfection are not finite. Opening the finite-infinite relation is an age-old enterprise so we close that door rather quickly with this simple definition of the infinite: It is the qualitative expression of continuity, symmetry and harmony whereby continuity begets order, symmetry begets relations, and harmony begets dynamics. The finite is the quantitative expression. That’s it. Nothing more.

Anything else anybody wants to impute is their business; it is probably not relevant here.

The Results. Within a little over one second, the base-2 expansion is out to the 144th notation. Planck Length is 360,424.632 kilometers. Planck mass is a hefty 4.8537×1034 kilograms. Just to put that in context, the mean average distance between the earth and the moon is 384,402 km (238,856 mi). It is 356,500 km at the perigee and 406,700 km at the apogee. The sun’s weight is around 1.989 × 1030 kg so at this notation, the density of the universe is like a neutron star.

The universe as we know it begins to take shape between Notation-196 and 197. Here the universe is at 10,829,559,004,640,000 seconds or about 343.15 million years.

Just within these 202 notations are a few highlights of this base-2 model:

• One second, between Notation-143 and 144,
  Planck Length is 299,792± km.
• One year is between Notation-168 and 169.
• The first 1000 years is between Notation-178 and 179.
• The first million years is between Notations-188 and 189.
• And, the first billion years is between Notations-198 and 199.

This model is primarily about the very early universe. Within the process, while it is being filled with planckspheres and with the emergence of geometries from the simplest to the increasingly complex, a five-tetrahedral cluster will manifest.

Although Aristotle thought it was a perfect configuration [16], and that understanding had been perpetrated by scholars for over 1800 years, the truth became apparent in the 1500s. Yet, even at that point, the real realities remained under-reported and less understood. As recently as the 1950s, chemists who recognized Aristotle’s mistake, calculated that size of that gap. It is an important gap.

Pentagonal, icosahedral and Pentakis-dodecahedral structures have such a gap or the surfaces are stretched and the internal angles are not exactly 60 degrees. In the 1960s the first concepts around aperiodic tilings were introduced. In 1976 Roger Penrose introduced his unique tilings and Alan Mackay followed up experimentally to show how a two-dimensional Fourier transform (with rather sharp Dirac delta peaks) manifests a fivefold symmetry. In 1982 Daniel Shechtman began his public-struggle to open the exploration of quasicrystals. This struggle to understand these geometries are current and on-going.

Pentagonal faces introduce new dynamics. The most fundamental dynamic would be the beginning of quantum fluctuations and its aftermath, undecidability (subject), uncomputability (relation), and unpredictability (object).

We are in search of answers to the question, “When and where do these fluctuations manifest?” We’ve beg for help. These are all new studies for us. Our simple history begins in 2011. Our critical history didn’t really begin until 2016. Notwithstanding, we are speculative people and believe the fluctuations actually and measurably begin to fluctuate, first between notations somewhere above Notation-64, and then between sets of notations, and within groups of notations.

Our Fuzzy Universe. In 1945 John Wheeler (Princeton) and Richard Feynman (Caltech) proposed quantum field theory or QFT, and, it has increasingly become a bedrock of physics [17]. Very well-defined, it can be argued that QFT has the deep roots to the unpredictable and indeterminate within the sciences, mathematics, and even logic, linguistics, philosophy, and consciousness. However, those within QFT studies have not yet considered the 202 base-2 notations and the implications of Planck base units, an exponential universe, a dynamic finite-infinite relation, and the dynamics of a structural evolution from the sphere and cubic-close packing of equal spheres. Within this model, the old epochs of big bang cosmology get readily absorbed by an all-natural inflation. There are at least eighteen very special claims that provide a possible foundation for QFT that deepens its roots and broadens its reach.

Gödel’s constructions.[18] Gödel gives Newton’s absolute time a place within General Relativity. And, given Einstein’s special relations with Max Planck, we are still in search of any references where Einstein or Gödel engage the Planck base units. Though Gödel was a teacher-professor (1940-1978) at the Institute for Advanced Studies and Einstein and Gödel had long walks, the infinitely-hot big bang probably got in the way. Even with Gödel work on numbering and base-2, he did not clearly demarcate a beginning of the universe.

Conclusion. We will continue asking scholars about our simple configuration as we learn more about those topics required to make our universe work. Thank you. –BEC 

Endnotes, Footnotes, References, and Resources

[1] Decidability (Subject). A key to this theory and construct (Wikipedia) is the coherence of its logic. Are Planck Time and Planck Length the smallest possible units of space and time? Some scholars say it is. By starting at those Planck base units, does that base-2 progression necessarily include everything, everywhere, for all time? Max Planck never applied base-2, so he was not able to declare the base-2 progression of doublings to be a logical system. We do. It is totally predictive. One validation point is between the 143rd and 144th notation; it logically confirms the distance light travels in one second. That number is 299,792 km and it is within .1% of the speed of light confirmed within the laboratory. That requires a certain coherence of our four most-basic natural units, those Planck units, and their dimensionless constants. That would include c with special relativity, G with general relativity, and ħ with quantum mechanics. Also, there is ε0 (vacuum permittivity) with electromagnetism and kB (Boltzmann constant) with temperature/energy). More…

So we now explore, “Does this qualify to become a first-order theory of Euclidean geometry (Wikipedia)? Do we start with Tarski (1949) and go to Hodges (Stanford Encyclopedia of Philosophy, 2018)?” How do we engage the first-order theory of Abelian groups (W.M. Szmielew,1955), and the first-order theory of hyperbolic geometries, (Schwabhäuser, 1959)? Stretching well beyond our comfort zone, we also explore Petra Wolf’s From Decidability to Undecidability by Considering Regular Sets of Instances (2019). Within our radically relational model, the subject is always derived from the totality or relations that defines it uniquely. These discussions will continue; check the links that open more…

[2] Computability (Relation). The question is asked, “Is it possible that computable functions, including Turing degrees, are not necessarily set within just Notation-202? In this model where space and time are derivative, computability theory logically begins within Notations 0-to-1 and builds logically to include Notation-202. The algorithms of computational logic, like dimensionless constants, do not necessarily reside within machines. Questions about the mind and consciousness are stretching us to start a theory of computation that logically starts within Notations 0-1 and grows to Notation-202. More…

[3] Predictability (Object). Because the only notation that has a past and future is Notation-202 —all others are complete, yet fully dynamic and fully symmetric — there is still change. That thrust for change is a dynamic that effects every notation. To begin to enter this intellectual space, some of the more recent work regarding predictability is being engaged:

• Predictability limit of partially observed systems, Abeliuk et al (Jan. 2020)
• Predictability, complexity and learning, William Bialek et al (July 2000)
• Decomposing predictability, Hofmann et al (Dec. 2019)

Within this model, time is finite and derivative. More…

Transmogrification: Starting with Notation-1 and going as high as Notation-67, logic prevails, yet our universe remains opportunistic. There is a thrust for more continuity, symmetry and harmony, reaching for a higher perfection. The first ten notations have been generally associated with Plato’s forms which today are associated with the automorphic forms of Langlands programs and string theories. Essentially this is the first-order of the planckspheres. We hypothesize that the next set of notations are a second-order for structures and a third order of planckspheres is for substances in the spirit of Aristotle’s Ousia. The emergent face of forms, structure and substance is qualities, the fourth face of the planckspheres. Perhaps as early as Notation-40 the first group of five-tetrahedrons, twenty tetrahedrons (icosahedron), or sixty tetrahedrons (Pentakis-dodecahedron) are manifest. When there is an ordering within the system, that gap, a squishy geometry, creates the indeterminant. We are projecting that transitions between Notation-50 and Notation-67. That’s a guess. More…

[4] Undecidability (Subject). Within this idiosyncratic model of the universe, there is a deep respect for the scholarship that provides us with a list of undecidable problems (computability theory) and the list of statements independent of ZFC whereby the transmogrification induced by the pentastar gap provides a different look at that concept that quantum logic is undecidable (Fritz, 2016). More…

[5] Uncomputability (Relation). The historic brain-mind discussion will be part of these discussions. The Mind, that is, all minds, are currently projected to emerge within Notations 50 to 60 while consciousness as we understand it today would always be within the current time within Notation-202. To begin to grasp the boundaries conditions between computability and uncomputability we are engaging many documents including:

• Uncomputability and complexity of quantum control, D.I. Bondar, A.N. Pechen, Jan 2020
• Uncomputability of Phase Diagrams, Johannes Bausch, (Oct 4, 2019)
• Uncomputability and free will, C. S. M. Nayakar, R. Srikanth (October 2012)

Perhaps the most illusive and difficult of all our studies, of course, there will be more…

[6] Unpredictability (Object). In 1970 I became enamored with the work of John Bell at CERN labs in Geneva. He had a new way of looking at the EPR Paradox. In time I went to meet him stopping along the way to visit with David Bohm and Carl Friedrich von Weizsäcker. My goal was to better understand how the relations could be the primarily real within the subject-relation-object formula. It was only by making space and time derivative did the simple formulation of continuity-symmetry-harmony, a moment of perfection begin to open up. We wanted a container universe but did not discover the container until 2011. Now, all these articles are beginning to make some sense. Unpredictability is built into the very essence of geometries of the universe, yet the universe itself can be profoundly knowable. Freedom, creativity and moments of perfections are all built into the structure of unpredictability. Though it is not the fundamental structure, it intersects with the most fundamental. So, to help better understand this nascent model, we continue to explore a few related articles:

• On the unpredictability of individual quantum measurement outcomes, A.A. Abbott, C.S. Calude, K. Svozil, 2014
• Unpredictable Planning Under Partial Observability, Michael Hibbard, Yagiz Savas, Bo Wu, Takashi Tanaka, Ufuk Topcu, 2019
• Bell nonlocality, signal locality and unpredictability, Eric G. Cavalcanti, Howard M. Wiseman, 2009

These are new studies for us and we have “miles to go” before it all coheres. More…



[7] The story behind this story. There are links throughout this website to the December 19, 2011 story of our high school geometry students and their teachers who chased tetrahedrons and octahedrons down into the Planck scale and then out to the age and size of the universe. Here are other key links to tell a bit more of that story:

• The STEM tool story tells even more stories. There will on-going analysis of lack of feedback from editors and scholars around the world.
• When we could find no place within our grid for Plato’s Eidos and forms, Aristotle’s Ousia, binary operations, axiomatic set theory, pointfree geometries, Langlands programs and string theory (please see line 11 of our horizontal chart), we decided, “That’ll all be within the first 67 notations.” We knew then there would be an endless amount of work to do within this model.
• The advantage of youth and naïveté resulted in this early story about our work together.

Naïveté is often a curse; but in this instance, it allowed our most simple concepts to emerge. More…

[8] Grand Reductionism. We started as everything does — simple. We take very little steps and ask simple questions. We try to respect the scholarship that has gone on before us. When we become confused, we step back to something more simple. So, it was with deep respect that we engaged the CDM approach to the universe and Steven Weinberg and his book, Facing Up. Yet, we could not imagine a larger “grand reductionism” so, we did wonder!

We continue wrestling with his work and with these other scholars:

• Beyond the Dynamical Universe: Unifying Block Universe Physics and Time as Experienced, by Michael Silberstein, W. M. Stuckey, Timothy McDevitt, Oxford (2018) Also: https://www.relationalblockworld.com/
• In 1979 I first met Steven Weinberg at his office in Jefferson Laboratory at Harvard. He had not received his Nobel prize, but The First Three Minutes was out. Everybody fights for their legacy.

We all need to fight for the deepest truth. More…

[9] Triangulations. Our initial studies of the work of F. C. Frank (H. H. Wills Physics Laboratory, University of Bristol, England) and J. S. Kasper (General Electric Research Laboratory, Schenectady, N.Y.) opened the concepts within cubic-close packing of equal spheres, the triangulated coordination shells, and the emergence of the tetrahedron from just four spheres. That all opened the way to engage The Physics of Quasicrystals, World Scientific, 1987 edited by P J Steinhardt and S Ostlund. We struggle to grasp the work of scholars within this area:

• Objections to set theory as a foundation for mathematics
• Jonathan P. K. Doye and his group are very helpful

Continued study follows here…

[10] Fourier. Our first introduction to the Fourier transform was through Steven Strogatz on Pi day in 2015. His article for The New Yorker Magazine resonated at that time and it still does today. Now we are attempting to really dig into the Fourier work. Of course, we have a long way to go. Here are some of the scholars to who we are currently turning for help:

• Danylo Radchenko, Maryna Viazovska, Fourier interpolation on the real line
• Martin Stoller, Fourier interpolation from spheres (ArXiv – 2020)
• The double Fourier sphere (DFS) method (Wikipedia)

A huge study, we have barely scratched the surface. More…

[11] Lorentz. Linear transformations are part of the dynamics within a notation. Yet, there is a homogeneity with all the contiguous planckspheres so geometries may readily extend within notations and across notations. It seems that the dynamics of all geometric models of the universe may hold insightful keys. With that mindset, we are open to all studies of space and time symmetry:

• Lorentz Transformation
• Rovelli: Reconcile Planck-scale discreteness and the Lorentz-Fitzgerald contraction
• Planck scale space time fluctuations on Lorentz invariance at extreme speeds

There will always be more…

[12] Poincaré. In 1980 I worked with Jean-Pierre Vigier and Olivier Costa de Beauregard at the Institut Henri Poincaré. Our focus was solely on the EPR paradox, Bell’s theorem, and the experimental work of Alain Aspect at the SupOptique or “IOGS” in d’Orsay (just outside of Paris). Never did we look back at the work of Henri Poincaré. Today, a focus is on the Poincaré sphere and its underlying Lorentzian symmetry as a geometrical representation of Lorentz transformations. More work with these scholars:

• The Poincare Conjecture: In Search of the Shape of the Universe, Donal O’Shea (2007)
• Sphere in Various Branches of Physics, Tiberiu Tudor (February 2018)
• Harmonic Analysis on Symmetric Spaces—Euclidean Space, the Sphere, and the
• Poincaré Upper Half-Plane, Audrey Terras, Springer Science & Business Media, 1985, 2013

[13] The Infinitesimal Sphere. Also called the Planck sphere, it is a key, core concept and we will continue to research it until we find the best possible resources that go back as early as possible. To date, we start with John Wheeler’s work with quantum foam believing that it could hold a key. Others are:

• Discrete Model of Electron, April 2019, DOI: 10.13140/RG.2.2.28408.49920, Discrete Universe Project, Jose Garrigues-Baixauli, Universitat Politècnica de València, Spain PDF
• Physical Significance of Planck Length, Thanu Padmanabhan, Ann. Phys. 1985 165(1) 38-58
• Also, see Planck Particle: https://en.wikipedia.org/wiki/Planck_particle

We continue wrestling with the work of scholars within this domain, so there will always be more…

[14] Automorphic forms. We turned to the scholars within the Langlands programs and string theory to learn about automorphic forms. We are learning about Loop Quantum Gravity n . They have done sustained work since the 1970s and have done a major amount of work to define its automorphic forms:

• Automorphic forms (Wikipedia) “One of Poincaré’s first discoveries in mathematics, dating to the 1880s, was automorphic forms.”
• Langlands program (Wikipedia)
• Is there an analytic theory of automorphic functions for complex algebraic curves?, Edward Frenkel (ArXiv – December 2018)

We continue wrestling with the work of scholars within this domain, so there will always be more…

[15] String theory. One of the world’s leading scholars within string theory is Ed Witten. He is also a gentleman. Because the majority of his career has been in the shadow of big bang cosmology, his work has had an impossible starting point with which to contend. There is no easy migration to a theory that pushes time-space-and-light together at the Planck scale, and then with mass-and-charge at the next level (c2). It will be fascinating to see if they will do better within a cold start that redefines the historic æther, and gives their discipline the radius of the plancksphere within Notation-1 and every plancksphere through Notation-67, and at least the first 67 notations of each subsequent notation.

• The logarithmic equation of state for superconducting cosmic strings, Betti Hartmann, Brandon Carter, November 2008 arXiv:0803.0266
• Seiberg–Witten invariants

We continue wrestling with the work of scholars within this domain, so there will always be more…

Of course, base-2 is the first exponential expansion of this model such that no point within the universe, right from the first instant, is more than 202 notational steps away. Yet, I believe our opportunistic universe will also test base-3 which would aggregate a 67-step shortcut through to Notation-201. Base-5 would provide a 40-step shortcut through to Notation-200. Base-7 would provide a 28-steps to Notation-196, base-11 just 18 steps to Notation-198, and base-13 just fifteen steps through to Notation-195. These clusters of notations possibly can introduce even more complex functions.

The largest square of a prime, 13¹³ is 169, obviously under 202; and, 17¹⁷ is over (289). More…

[16] Geometric gap. One of history’s greatest thinkers made a most fundamental mistake that was repeated for about 1800 years. That is a tragedy of epic proportions. We are all taught to have such great respect for scholars, sometimes it holds us back. Aristotle (384–322 BCE), one of the greatest Greek philosophers and a polymath obviously had imperfect models of the tetrahedron, otherwise he would have seen and felt this geometric gap. Five tetrahedrons all sharing one common edge opens that gap.

My first discussion about it was in 2016.

1800 years. The greats that followed him repeated his mistake and we failed to grasp a most-essential quality of simple geometry. One of our primary source article is “Mysteries in Packing Regular Tetrahedra (PDF)” by Jeffrey C. Lagarias and Chuanming Zong. They relied heavily on the Dutch article by D. J. Struik, Het Probleem ‘De impletione loci’, Nieuw Archief voor Wiskunde, Series 2, 15 (1925–1928), no. 3, 121–137. Two chemists, F.C. Frank and J.S. Kasper with their article, Complex Alloy Structures Regarded as Sphere Packings, took it further and calculated that gap. An key part of it all is the work of Daniel Shechtman, I. Blech, D. Gratias, and J. W. Cahn, Phys. Rev. Lett. 53, 1951 (1984). https://doi.org/10.1103/PhysRevLett.53.1951, Google Scholar Crossref

We are among a very few who claim that this gap is the basis for quantum indeterminacy, imperfections, free will, unpredictability, undecidability and uncomputability, so there will be much more to come…

[17] Fuzzy Universe. The concept of a warm and fuzzy universe certainly flies in the face of current cosmology and even with the physics that has grown out of the work of people like John Wheeler and Richard Feynman. Yet, perhaps we have the makings for a mathematics of a hyperconnected universe. Let’s open it up for discussion. Let’s see if our universe is as hyperconnected as the internet and our brain. More…

[18] The Constructions of Scholars. Three of our foremost scholars of history, Aristotle – Newton – Hawking, all made mistakes. They were human. They were also lifted up so high, nobody within their time could allow them to fall or fail.

Aristotle’s mistake was so ingrained and so pivotal, quantum fluctuations have remained a mystery to this day. Here the belief that physics is geometry bears out in a most simple way to explain a most difficult concept.

Newton’s absolute space and time held back scholars with a deep understanding of continuity, symmetry, harmony, and yes, even beauty. The infinite became a place where only fools dared to tread.

Hawking was trapped by his disease and by becoming a Lucasian professor. He couldn’t deny Newton. Had he, perhaps he would have been moved to redefine the infinite as continuity (order), symmetry (relations) and harmony (dynamics) whereby space and time would have become derivative and relational.

Even with his work on numbering and base-2, Gödel never applied his logic to a base-2 model of the universe from Planck’s units to the current time. It is our loss. More…

###

---