CENTER FOR PERFECTION STUDIES: CONTINUITY•SYMMETRY•HARMONY • GOALS • September 2019 HOMEPAGES: ASSUMPTIONS|DARK |HOME|INFINITY|Inflation | KEYS|MAP|Transformation

We’ve been “top down” too long.

Let’s try to build from the “bottom up”
to grasp those first 64 key notations.

by Bruce Camber, Autumn 2019

Abstract. Please take as a given that our conceptual foundations begin at the Planck scale and extend to include the current expansion of the universe today, right Now. Also, take as a given that the entire universe — everything, everywhere, for all time — is mathematically encapsulated within 202 base-2 dynamic doublings from the Planck scale.1 It is a simple mathematical fact. There are no less than 64 base-2 notations or doublings of the Planck base units before the elementary particles and waves begin to emerge. Could this be a new working model? To explore it further, we take the mathematics as a given. This very different reality seems to require that we do the following: (1) redefine space-and-time, (2) define a finite-infinite bridge, and (3) redefine the infinite. A new domain of mathematical physics and logic begins at the first notation and proceeds at least 64 notations to the edge of today’s research within 2019 and CERN’s scale of particles & waves). If true, these first 64 notations will become the beginnings of a paradigm shift.

Very, Very Brief History

Democritus (circa 400 BC) is often given the title of “the world’s first scientist” because he was the first to have an atomic theory of matter. Yet, only in 1745 did a less-well-known scientist, Ruggiero Giuseppe Bošković, lay foundations for our modern atomic theory when he published De|Viribus|Vivis.² Then, in 1897 J. J. Thomson defined the first subatomic particle,³ the electron. Though the rest is well-documented history, with all our advances in technology, especially the power and precision of computers since the 1960s, the essential structure-and-ideation of current theory has not substantially changed. Yes, in 2012 the hadron was formally added and all the related concepts have been well-ordered within the Standard Model for Particle Physics, yet the basic problems of unification of physical theories stubbornly persist.

There has to be a better way.

___________________________________ Start at the bottom

To start at the bottom, we will have to ask, “What is the simplest concept with which to begin?” …a point? …a line? …a triangle? …a ratio? Conducting my own informal survey for over 40 years, the judgment rendered is the sphere.⁴  Yes, a sphere! So, I took it as a given that the sphere is the most-basic building block of our universe and began to explore all things circular, spherical and related to pi (π). With just pi in this toolbox, how do we build a universe? Ever-so-slowly, we began to realize those first 64 notations or doublings from the Planck scale held the keys. This chart of the universe ⁵ of just 202 successive doublings of the Planck base units, by definition, encapsulated everything, everywhere, for all time within a very special base-2 container. It is mathematically-defined and fully-integrated. It is exponential and has an all-natural inflation. Of course, this is a very different structure within which to study possible details of our universe, especially the earliest universe. It is assumed that every number within our horizontally-scrolled chart can be studied and tested against actual numbers throughout the sciences, including the rather complex mathematics of string theory, Langlands programs, renormalization schemes, particle physics, and astrophysics.

The key question: How did that first sphere come into this picture?

The finite-infinite bridge.⁶

Within our earlier analyses, we made a substantial assumption that the origin of the finite is the infinite. The never-ending numbers of pi have to come from somewhere. Yet, it became obvious that we would have to redefine the infinite and more carefully define those concepts that create bridges between the two. Just what is a “never-ending, never repeating” number and why is pi (π) the most ubiquitous? What are dimensionless constants?

If it it is not defined by space and time, it is not fully finite.  If it somehow defines space and time, yet is not finite, how can it be infinite? To move forward, we considered pi to be our initial definition of the infinite. Next, we considered those Planck base units as a starting point; any “measurements” that are smaller, would define “the bridge.”

And, all other dimensionless constants must span the bridge. That’s our start.

The infinite:⁷  What qualities of infinity manifest as pi (π)?

My answer: Continuity (order), symmetry (relations), and harmony (dynamics).^7a Beyond this initial definition, other dimensionless constants are necessarily added. Experts suggest there are 26-to-31 such constants necessary for the Standard Model of Particle Physics.^7b Others suggest even more dimensionless constants.^7c On the finite side there is electromagnetic and gravitational radiation, both defined through the Fourier transform within every circle and sphere.^7d We are learning more every day to attempt to take this construct beyond our initial hypotheses. Yet, as a given, we extend our basic hypothesis to include all the deepest dynamics of spin and rotation.

Sphere stacking, Cubic-Close Packing, Period Doubling, Fourier Transform

At least four functions define the Planck base units.⁸ Starting with π (pi), our ubiquitous, never-ending, never-repeating number, we work up to the simple definition of that very first sphere. But now, we have exceptionally small numbers to plug into those formulas to define the very first moment of space (Planck Length), time (Planck Time), mass (Planck Mass), and energy (Planck Charge). The mass and charge of that sphere are measurable. We will not be able to measure a fractional unit of length until around the 65th notation (doubling). We will not be able to measure a fractional unit of time until our 84th notation, yet forms and functions are now emerging (See A, a dynamic image on the right) from the first notation.

Although not yet a generally-accepted scientific term, that very first sphere, in honor of Max Planck, is called a plancksphere; and, here it is the assumed to be the very first definition and moment of physicality-and-time. It appears that sphere stacking and cubic-close packing capture the form of this expansion and the Fourier Transform captures the function. Period doubling might negotiate the ratio between form and function. 

The first ten notations.⁹

We double the Planck base units, then double them again and again. This generation of Planck spheres — 2, 4, 8, 16, 32, 64, 128, 256, 512, and 1024 within the first ten notations is never ending, constant, and now. By definition this generation of these spheres is faster than anything else in the universe, perhaps as high as 10⁴² spheres per second (if our simple vertex count — 2.78759×10⁴² — is anywhere close to right).

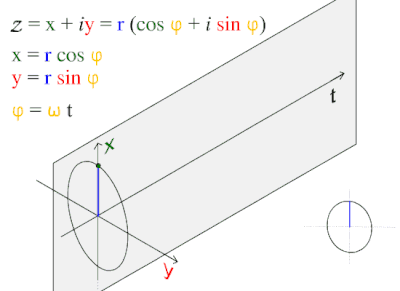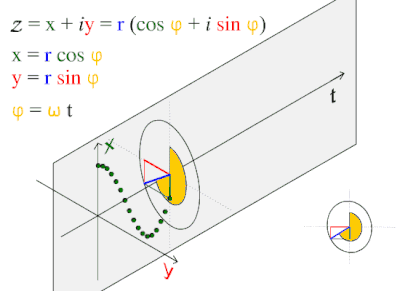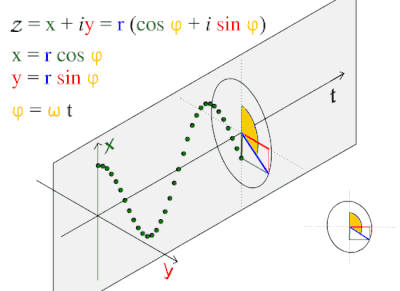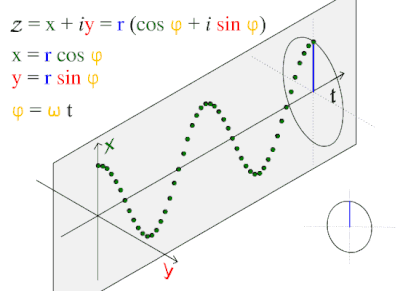
So, densities are extreme; sphere stacking instantaneous; and, the simplest geometries (as illustrated just above in A) naturally build upon each other.

Notations defined by prime numbers — 2, 3, 5, and 7 — open possibilities for a progressive addition of dimensionless constants, i.e. ‎Buckingham π theorem and pure numbers, i, e, and φ. Natural functions (i.e. anisotropy) within these forms are being studied. A question being addressed is, “Could there be a hypostatic period doubling bifurcation (B) that is a natural expression of sphere stacking (A)?”

Another natural function is the Fourier transform and it has at least two expressions defined by its cosine wave. Part of the necessary definition of the sphere is the cosine wave’s fundamental relationship to the circle (C and D); it is dynamic, inherent, and always. These dynamics are within the mathematics that are the very definition of circles and spheres. Yes, all four graphical illustrations, A-to-D, capture part of the dynamics that are part of the requisite definition of a circle and sphere.

Though hypostatic — not measurable within space or time — these basic building blocks are constantly defining space and time. Our one-word description for this domain of ten notations is Forms or Eidos.

The next fifty-three notations, 11-64:¹⁰ 

Back in August 2017, we did a very preliminary, highly-speculative, introductory analysis of Notation 31 as part of a sampling across the entire 202 notations. At the 31st notation the mass is 46.79 kilograms (about 103 pounds); there are already 1.237 octillion or 1.23794×10²⁷ scaling vertices all within 3. 470762×10^-26 meters. To be able to begin to grasp those numbers, we initiated a study of the densities of neutron stars. We learned that such densities are indeed measured today.

We became highly speculative and began imputing values to a range of notations. From 31-to-40 we hypothesized it to be for the emergence of Qualia or primordial Qualities (which build upon notations 21-to-30, primordial Substances. These notations build up from 11-20, primordial Structures. We intuited those ranges back in 2014. Possibly just a fantasy, we acknowledge these ranges are just placeholders against which to develop more appropriate categories.

Going larger, the range of notations from 41-to-50 is reserved for primordial Relations, and 51-to-64 is reserved for primordial Systems. Within this simple logic and philosophical orientation, we are  trying to discern when string theory and the mathematics of Langlands programs emerge including the ATLAS of Finite Group Representations,  E8, and the Sophus Lie group.¹¹

There can be nothing exempt from this chart, so even the most complex and far-reaching constructions within our intellectual history must be included. It won’t be easy for most of us but I have great faith that our mathematical wizards can make it all magically simple!

Notations 65 to 84.¹²

This range includes the Periodic Table of Elements and the Standard Model for Particle Physics. Each number of the 202 notations is the number of times the Planck Length (and each result) has been doubled. The 20th century model of the universe once began at 10^-10 meters (our Notation 83); and until recently, the generally-accepted model only went down to 10^-15 meters (our Notation 66). Again, when we apply base-2 exponentiation to the four Planck base units, there are a total of 202 notations that outline our universe. Each notation necessarily builds on the prior whereby the first moment of time is defined by the Planck base units, beginning a natural inflation, an expansion that defines the current time, The Now.

Bottom Up? Will we ever see light?

Covered by layer after layer of Planckspheres. Visible light manifests within Notations 94 and 95. It has a narrow notational spectrum. Yet, gamma rays at about one picometer and radio waves at 100,000 kilometers hardly come close to the first ten notations of the Planck base units or the last ten notations up to the current notation.  The naming conventions for the extension of the electromagnetic radiation are part of the puzzle and suggestions are most welcomed. Metaphorically, it would seem that we are buried in planckspheres. Though infinitesimally smaller than elementary particles, there is still some light at the end of this tunnel, however, we are still trying to discern the best path to it.

Starting at the bottom is always difficult. Yet, we do. We all do. We are not born with depth of knowledge or experience. The important mindset to keep, even as we do acquire knowledge and perspective, is to keep our minds open. Arrogance is deadly. It stops us in our tracks.

Although we are confident that these 64 notations are keys to a paradigm shift, we are also so naive and unsure of ourselves that we need to hear feedback from professionals. So, to that end, we will try again to get some articles published and emails answered..

###

The priority will be:  (1) a compilation of this article and three others:  A Simple Model – 12 points absorb the universe in 202 steps,  Transformations – Cubic close packing, period doubling, Fourier transform, and Map of Our Universe; (2) an article currently being developed (still rough), and others that have already been rejected,  “New STEM tool delights, but raises questions” and  “Dark Matter & Dark Energy — Not Dark.”

###

Endnotes, Footnotes, References and Resources

¹ 202 doublings.  Our horizontally-scrolled, mathematically-integrated Chart of the Universe began in the geometry classes of a New Orleans high school with just a base-2 (doublings) expansion of the Planck Length. In 2014 Planck Time was added and in 2015 Planck Mass and Planck Charge.  To more readily follow the numbers, in 2016 the entire chart was laid out horizontally. It was first considered to be our own homemade STEM tool; however, the first 64 notations have been a mystery.

Is this where hypothetical particles are postulated (often just a mathematical convenience), concepts such as axions, inflatons, instantons, and a host of other preparticles?

We’re still asking experts about this model. Most of our correspondence has been to scholars. All are asked, “What’s wrong with our little STEM tool?

____________

² P. Ruggiero Josepho  Bošković, author of De Viribus Vivis. Prior to doing the research for this article, I did not know the work of Boscovich from Ragusa (Dubrovnik, Croatia) or about his De Viribus Vivis. He is not even given a line within Wikipedia’s recounting of Atomic Theory. The more familiar names of Proust, Dalton, and Avogadro are among those who open the way for the Bohr model, then the work of de Broglie, Heisenberg, Dirac, and Feynman. Ostensibly our model today has not changed for well over 100 years. It’s been refined. Beginning with these endnotes, I will continue learning about how the essential character of atomic theory evolved from Boscovich through his attempt to create a synthesis between between gravitational theory by Newton and the monadology developed by Leibniz. It is the Leibniz-Clarke correspondence all over again.

____________

³ Subatomic particles.  Preparing this article has been a good review of the history of physics; I had forgotten that J.J. Thomson opened the way to subatomic particles as early as 1897. The entire history around the electron is important because it helps to get perspective on why the work on the base units of time, length, mass and charge by George Stoney and Max Planck were found to be a little more than a curiosity or novelty than a new strategic tool. Also, in light of the fact that Newton got the upper hand over Leibniz back in 1716 when Leibniz died, absolute space and time had become accepted realities, an infinite platform within which everything can become a thing. Subjects and objects are real entitive realities and thingness is key.

____________

⁴ The Sphere. Major parts of the mathematics of the sphere within these 64 notations have already been done. Orienting those studies to the sphere and to infinitesimal space and time have not. Of course, I am referring to the purely mathematical studies at the Planck scale, mostly since the late 1960s, within the string theory community and among those working on the Langlands programs. There have been some scholars who have tried to develop linkage between the two, but without the deep structure of the first 64 notations, no results have been found overly compelling and none have gotten substantial traction. Concepts like branes, d-branes, dilaton-dilatino, graviton-gravitino,  knots, p-branes, or preons are yet to find a place on the grid. With base 2, the prime numbers, and 64 doublings. I am confident that the scholars who own these concepts will be able to pull it all together and do so relatively quickly.

____________

⁵ A Chart of the Universe.  This chart is a map of a very dynamic universe whereby every notation is unfolding right now. All the notations are active and interacting. One might discover that our definition of self ultimately comes from every notation. Perhaps this chart will take on the character of Abraham Maslow’s hierarchy of needs whereby the most advanced among us will be able to discern the greatest number of manifestations of notations alive within our self-definition. While we are being speculative, why not be boldly speculative!?!

____________

⁶ The finite-infinite bridge.  Arguments about the infinite and infinity will not be resolved here. However, a relatively new concept is introduced; that of a finite-infinite bridge. Doing a search (Google) of “the finite-infinite bridge” rendered just five results and three of them are from this work.  It is not a “hot” or commonly-accepted concept.  Nevertheless, a finite-infinite bridge seems necessary if both are to be more fully understood.

____________

⁷ The infinite: The hypothesis is that pi (π) begins our definition of the meaning and values of the infinite.  The sphere continues that definition. The three forms/functions  of the sphere are continuity^7a (order), symmetry (relations), and harmony (dynamics). All three also define what makes us human, intelligent and creative. Within this mix, the experts add dimensionless constants, 26 from Joan Baez^7b (his best guess in April 2011) and 31 from Aguirre, Rees, Tegmark and Wilczek.^7c The National Institute for Standards and Technology^7d (NIST) has over 350 physical constants that add further texture. Wikipedia even has a list of dimensionless quantities.^7e All will find a place along this grid.

____________

⁸ Cubic-Close Packing, Period Doubling, Fourier Transform: There are four images that help us grasp the dynamics of these three well-known functions. Cubic close packing is a demonstration of sphere stacking (A) that takes us back to Kepler et al). It also demonstrates the first emergence of a space-time moment (that very first sphere), and the convergence from spheres to points, lines, triangles, tetrahedrons, and octahedrons. Within the first doubling we have already begun to see the emergence of Euclidean geometries and the generation of the most basic automophic forms. We have a long way to go before we can actually begin to measure a length at the 67th notation (doubling). That first measurable fractional unit of time comes later at the 84th notation. This is the domain of Langlands programs and string theory, yet here we have actual numbers and ratios and correlations of lengths, durations, mass and charge to plug into each of these mathematical constructs. The numbers are real, but only now will we begin to see how these are really real! George Stoney and Max Planck did not try to build a universe on their base units. That each was able to intuit that reality was genius enough for their time. In our time, right Now, perhaps the goal should be to bring the plancksphere alive and to begin a deeper definition of the first law of thermodynamics and the very nature of space and time.

_______

⁹ The first ten notations. There is so much to learn and so little time (our life is short). I’ll be working on this 1-202 chart until I die. Notwithstanding, the Buckingham π theorem is part of our understanding of homogeneity and isotropy; it’s the heart of dimensional analysis. The Buckingham π theorem takes π to the next level along with the pure numbers, i, e, and φ. It is a thrust in the intellectual direction that ratios and equations are real and the things of space and time are derivative.

So, yes, we will continue our studies of those pure numbers, i, e, and φ and  de Moivre numbers, as part of our work on the theory of group characters, and the discrete Fourier transform seeking to justify our belief that all these expressions of mathematics are inherent and active at the Planck scale.

Eventually we want to discuss how these 64 notations open up discussions of concepts within algebraic geometries, projective geometry, Euclidean geometries, category theory, Mandelbrot sets, Julia sets, Möbius transformations, Kleinian groups, S-matrix theory, unitarity, bootstrapping, Hermitian analyticity, the Golden ratio (Phi), the Fibonacci sequence, fluctuation theory, ratio analysis, and ring theory.

                                                                        ______

¹⁰ The next fifty-three notations, 11-64: Although the first ten notations are most foundational, there are clues within each of the puzzle pieces. There are particular equations, ratios or mathematical expressions that necessarily begin to be defined within just one of the next fifty-three notations. That will actually inform the first ten. Ultimately every notation will be a key to see how “everything, everywhere, for all time” integrates through each notation. The 2017 sampling of Notation 31 raised many new questions about our earliest universe when it has a total mass of just 46.79 kilograms (about 103 pounds). How in all creation could 1.237 octillion scaling vertices be meaningfully compressed within 3. 470762×10^-26 meters?  Even with our initial studies of neutron stars and with the help of leading scholars in the field, we were overwhelmed. The goal now is to attempt to discern particular benchmarks, expressions or factors within string theory and/or the Langlands programs that point to a particular notation up to that 64th notation. In 2013 the first Universe Table was created. It is a 12×12 inch tabletop version of our original 11×60 inch table. Dubbed the surfboard (because a colorwheel wrapped it so brightly), the first 64 notations were in groups of up to ten notations. The categories were determined by asking the questions, “What comes first? What is more simple?” Though unchanged since 2013, there is nothing to stop any changes when a better logic prevails. So, from automorphic forms with the first ten notations, a Hilbert and Bourbakian sense of structure defines notations 11-20. Perhaps a precursor to the Periodic Table, the notations from 21 to 30 define groups that will become her 118 substances. The next group, 31 to 40, is a bit unusual in that qualities (Qualia) has never been part of, or on, any grid. It just seems as the dynamics of the Fourier transform continue to “discover” a deeper variegation, that particular combinations could be defined as the precursor of a quality. Of course, there are many scholars and experts who will make sense of all these very simple concepts! Although simple symmetries have been part of the initial definitions of things, these are all still hypostatic. At some point, however, these symmetry groups may well define the precursor of a relation and throughout the next ten notations, symmetry groups begin to “discover” other groups and the precursor of relations emerge.  Then as symmetry groups further hypostatically organize, the precursors of systems emerge and here I would controversially include the Mind, all minds of every thinking thing. So, now we have so many precursors. It is incumbent on us to make these outlines come alive.

___________________

¹¹ E8 and the Sophus Lie group.  Extraordinary efforts at unified theories of everything often open the range and depth of possibilities. Garrett Lisi did as much with his 2007 E₈ Theory.  He stimulated many of us to learn about E8 and the Sophus Lie group. Many of us were reminded of how limited our education had been! Penetrating all the key concepts that are E8 mathematics, as well as E₈ lattice and the Lie group became a challenge.  Another dimension of this study includes what is known as the ATLAS of Finite Group Representations (Wikipedia).

What? What did we learn in school that day?

Yes, so to incorporate this specialized, far-reaching areas of knowledge, this project will seek out experts.

___________________

¹² Notations 65 to 84 Chaos returns to order (yet with major key questions unanswered) because with each notation we now begin to see the Standard Model for Particle Physics (Wikipedia) and then the Periodic Table of Elements. All accepted science and part of our sense of the definition of things, yet the prior 64 notations have great potential to help us to see things even more clearly and deeply and wholly.

___________________

Four Key Interrelated Pages:

1. Been “top down” too long. It’s time to build from the “bottom up”
2. A Simple Model – 12 points absorb the universe in 202 steps.
3. Transformations – Cubic close packing, period doubling, Fourier transform
4. Map of our universe – The most simple-and-comprehensive

---

Your comments and questions are encouraged.

---

History of this page:

• Privately posted on August 23, 2019 @ 4:04 PM
• Publicly posted on August 27, 2019 @ 18:01 PM
• Most-active editing, August 24-September 7, 2019 Last update: 10 March 2022
• Homepage: 30 August 2019 to  September 30, 2019
  

---

---

Reference & Resources & Working Notes

• For more study, go to these pages:
  https://81018.com/infinity-summary/
  Cubic close packing of Equal Spheres: https://en.wikipedia.org/wiki/Close-packing_of_equal_spheres#Simple_hcp_lattice Period-doubling bifurcation:  https://en.wikipedia.org/wiki/Period-doubling_bifurcation

• On the scaling structure for period doubling (PDF), Garrett Birkhoff, Marco Martens & Charles Tresser, Astérisque, Société mathématique de France, 286 (2003), p. 167-186

• Cosine relationship to the circle: https://en.wikipedia.org/wiki/Sine_wave#Occurrences
• Sine of a unit circle:  https://en.wikipedia.org/wiki/Sine
• List of trigonometric identities
• See search results: light, dimensionless constants
• Preparticles
• NATURAL INFLATION  https://arxiv.org/pdf/hep-ph/9207245.pdf Also: Fred C. Adams, J. Richard Bond, Joshua A. Frieman, Angela V. Olinto
• Adrienne P. Lamberti (2007) The Thingness of Things, Rhetoric Review, 26:4, 443-444, DOI: 10.1080/07350190701577967  https://soylentnews.org/article.pl?sid=17/07/30/1855218&from=rss 
• Young mathematicians have found a bridge across the finite-infinite divide, helping at the same time to map this strange boundary.   https://arxiv.org/abs/1601.00050   Theodore A. Slaman and Emanuele Frittaion
•  A. Eichhorn, H. M. Lee, S. C. Park, J. Rubio, A. Salvio, S. Sibiryakov, M. Shaposhnikov, A. Strumia, C. Wetterich
• Also: Steven Abel, Damiano Anselmi, Fedor Bezrukov
• John Donoghue, Astrid Eichhorn, Dumitru Ghilencea, Jinn-Ouk Gong, Christopher T. Hill, Bob Holdom, Deog-Ki Hong, Sang Hui Im, D. R. Timothy Jones, Elias Kiritsis, Archil Kobakhidze, Manfred Lindner, Anupam Mazumdar, Philip Mannheim, Hermann Nicolai, Kin-ya Oda, Roberto Percacci, Eliezer Rabinovici, Graham Ross, Javier Rubio, Alberto Salvio, Francesco Sannino, Kellog Stelle, Christof Wetterich

Images: