The Fourier Transform
by Bruce E. Camber, Initiated: September 2019 Updated: January 28, 2021
Background: Of all places, I intentionally started to learn about the foundational and ubiquitous nature of the Fourier Transform from a March 13, 2015, The New Yorker (magazine) within an article written by Steven Strogatz for Pi Day, March 14 (3.14), 2015. Perhaps it was a refresher of concepts learned in 1964; it felt like it was the first time. Surely it was the first time to see the Fourier in light of the 202 notations encapsulating our universe (by applying base-2 to the Planck base units). Here are key processes by which a concept changes the quality of our life and our understanding of the universe. You would not want to live without the functionality of the Fourier Transform! …nor could you.
We thanked the author, Prof. Dr. Steven Strogatz of Cornell University who said the following:
Continuities and Symmetries:
Keys to the Harmonies of the Fourier Transform
It is a package. We cannot have one without the others.
Scale Independent or scale invariant:
All circles and spheres need to be reconsidered for applications within the Planck scale. Because our little model is scale independent or invariant, all such images apply within the finite-infinite transformation and within the Notations 1-to 201. Because Notation-202 is still “in process” or asymmetric, that scaling may well be limited.
Sphere Stacking-Packing, Fourier A-to-C and Maybe D & E
Sphere Stacking-Packing: Discovered online in 2014, this image gave us the visualization of the transformation from spheres to interior functions and lines, and finally the Euclidean-Platonic geometries. This study, largely from within Wikipedia and the following Fourier-related dynamic images, are well-worth our time to reflect on them.
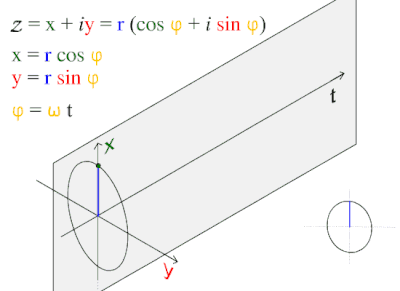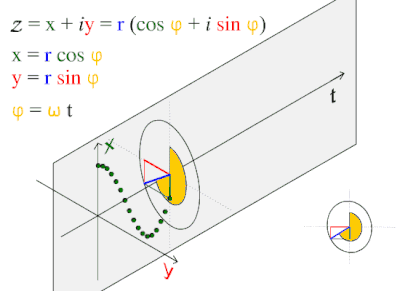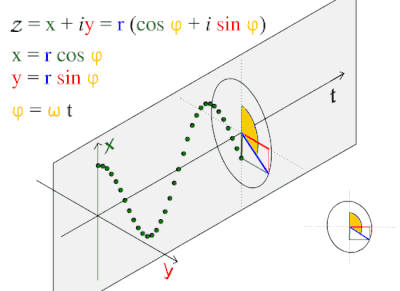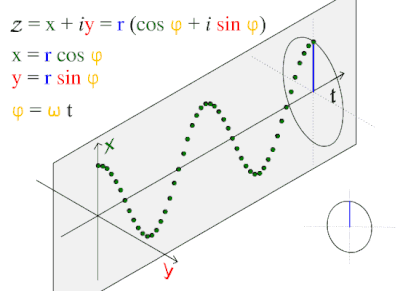Fourier A. “This wave pattern occurs often in nature, including wind waves, sound waves, and light waves. A cosine wave is said to be sinusoidal, because cos ( x ) = sin ( x + π / 2 ) , 
Fourier B. “The sine is a trigonometric function of an angle. The sine of an acute angle is defined in the context of a right triangle: for the specified angle, it is the ratio of the length of the side that is opposite that angle, to the length of the longest side of the triangle (the hypotenuse).”
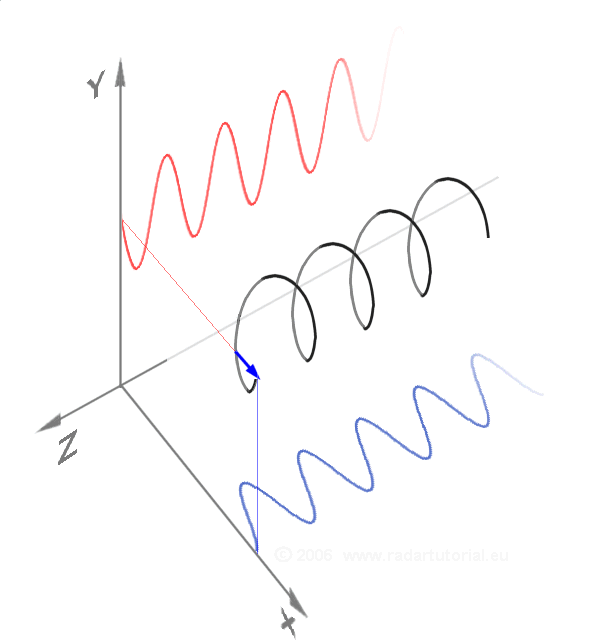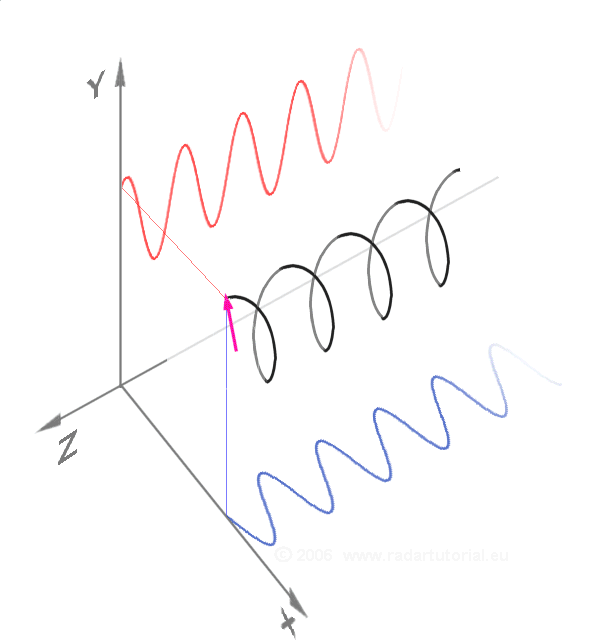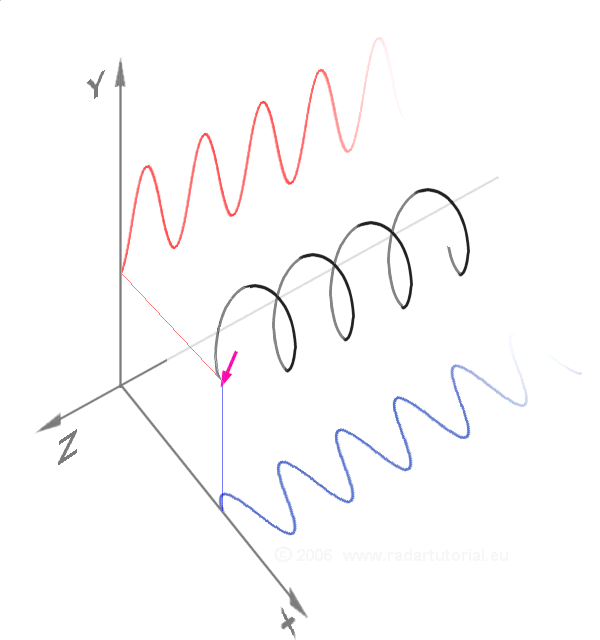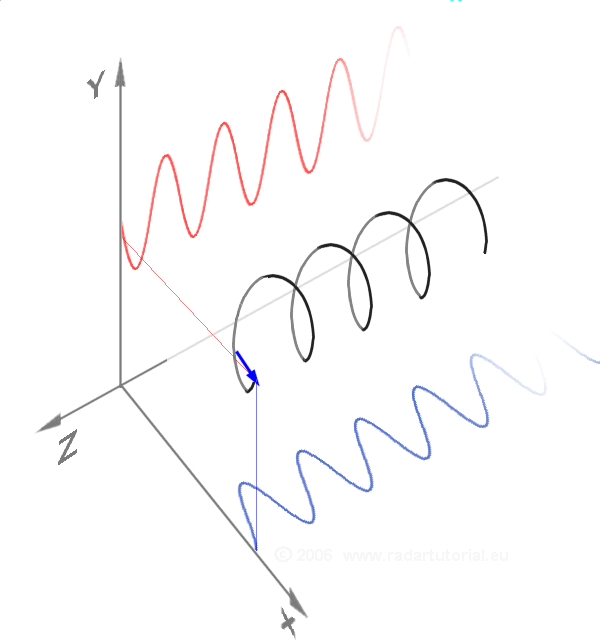Fourier C. “A circularly polarized wave as a sum of two linearly polarized components 90° out of phase.” Also, see the Poincaré sphere.
Possibly a Fourier D. “Animation showing four different polarization states and two orthogonal projections.” Also, see polarization states and circular polarization.
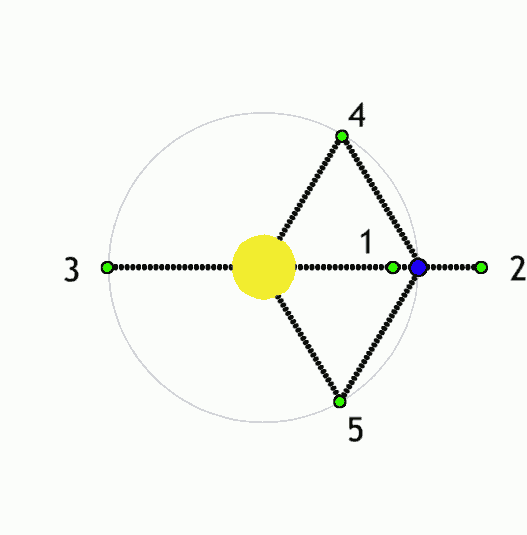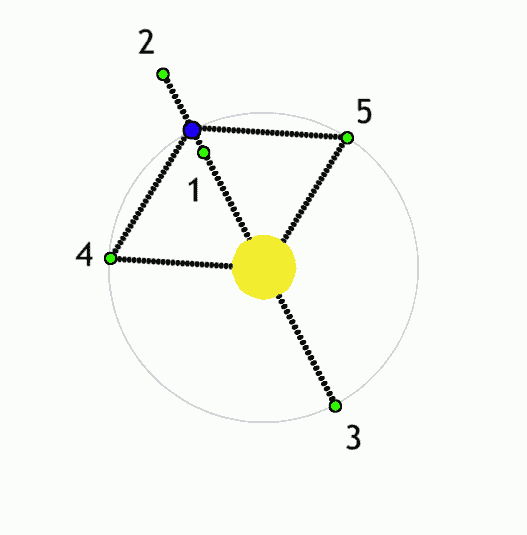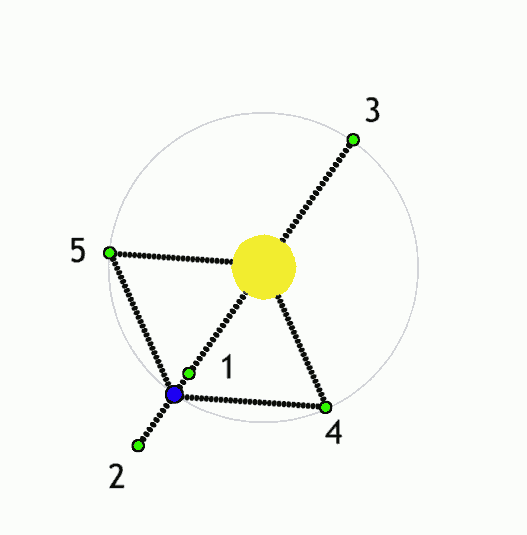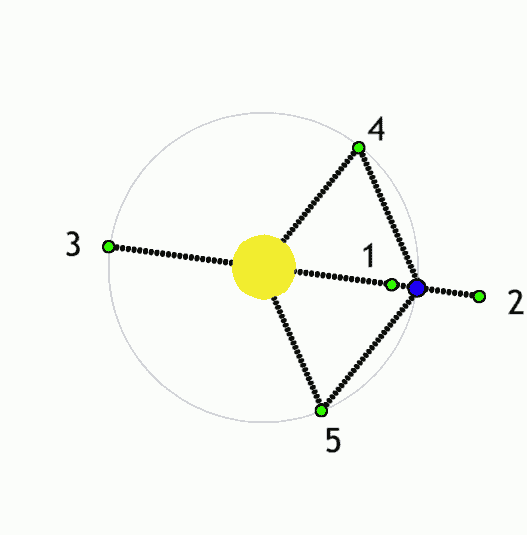Possibly a Fourier E. More speculatively, let us ask, “If the dynamics of pi are scale independent, might the Lagrange points within celestial mechanics be applied to the Planck scale? So, if we assume that Lagrange points describe activity at the Planck scale, within which notations might it first manifest?” A parts-whole question is considered.
Online Resources:
Video: Computing the Fourier series (MIT 18.03SC Differential Equations, Fall 2011), David Shirokoff, OCW, MIT, 2011. Special thanks goes to David (who has had outstanding careers at MIT, McGill).
Online Course: Differential Equations, OCW MIT Profs. Arthur Mattuck, Haynes Miller, Jeremy Orloff, and John Lewis.
Six easy roads to the Planck scale, Ronald J. Adler, Hansen Experimental Physics Laboratory (Gravity Probe B Mission), Stanford University, Stanford, California 94309
True confessions. We have learned to follow every lead. While getting further and further involved with the study of pi (π), we would slow down a little to make some guesses and postulations knowing full-well that we would be back to attempt to understand each function more deeply.
Symmetries in motion. The circle-sphere dynamics now transition from basic geometries, to symmetries in motion.
The work of a wide range of people, from Pythagoras (c. 570 – c. 495 BC) to Feynman (1918-1988) to Strogatz (1959- ) to today’s thinkers and tinkerers within music theory, may find a key function and a new paradigm within the Fourier transform understood from the Planck scale.
There is an inner transformation (pictured) that I would equate to electromagnetism, Maxwell’s equations and Faraday’s intuitions. Then there are the outer transformations which I would equate with the de facto dialogue between Newton and Einstein and the current wrestlings regarding our understanding of gravity and loop quantum gravity (LQG).
See Sir Martin Rees’ Just Six Numbers.
The internal and external dynamic of spheres. The three dynamic images above are each, in their very special ways, based on our most ubiquitous, never-ending, never-repeating, dimensionless constant, pi.
If in the first emergence there are endless strings of spheres, could it also be a face of Planck Charge, Planck Mass, Planck Length and Planck Time? If part of that emergence is the inner transformation of pi, in what ways is it the face electromagnetism and an expression of Planck Time, Planck Length, Planck Mass and Planck Charge? If another part of that emergence is the outer transformation, in what manner of speaking is this the face of gravity and yet another expression of Planck Time, Planck Length, Planck Mass and Planck Charge?
History will be a guide. How could so many applications not be tied to the fundamentals of our beginning?
The Fourier transform: Cornell mathematician, Stephen Strogatz, loves the Fourier transform and I thanked him for his spirited re-introduction to its place within science and with the functions of pi. If by starting at the Planck scale, the Fourier transform redefines electromagnetism and gravity, our best living scholars throughout the breadth and depth of all those applications will be encouraged to engage this construct.
Key Fourier applications just may be extended in ways to address age-old questions. I have a hunch that there are calculations between the inner and outer transformations that just might confirm Sir Martin Rees first number within his book, Just Six Numbers. It is the ratio of the strength of the electrical force to the gravitational force. Surely this might add an important twist to our understanding of gravity and charge and mass. More….
Fourier series, transform: The goal here is to bring everyday physics and mathematics to bear to grasp the foundations of our universe so there is nothing esoteric or extra-logical about it. How very satisfying it will be if key mathematicians throughout our history, people like Kepler, Gauss, Hales (cubic-close packing), Poincaré, Feigenbam (period doubling bifurcation), Fourier, Dirac, Strogatz (Fourier transform), and Planck are responsible for the concepts that describe and predict the behaviors within our infinitesimal universe.
ON THE FOUNDATION OF NONCOMMUTATIVE GEOMETRY. Although mathematicians before Gelfand had studied normed rings, it was he who created the tools that got the theory really started. In his thesis he brought to light the fundamental concept of maximal ideal and proved that the quotient of a commutative Banach algebra by a maximal ideal is always the field C of complex numbers. This easily implied, for instance, Wiener’s well known result that the inverse of a function with no zeros and absolutely convergent Fourier expansion also has absolutely convergent Fourier expansion. –Alain Connes
Of course, there will be much more to come…
Worldviews limit perspective 